-
Решения
-
Теория
-
Задачник
-
Идеи для учителя
- Заказать обучение
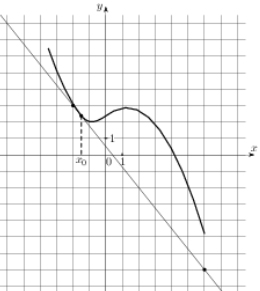
Значение производной функции в точке х0 равно тангенсу угла, образованного касательной и положительным направлением оси Ох (угол α)., т.е.
f'(x) = tgα.
Задача сводится к тому, чтобы найти tgα.
Смежный углу α будет угол β.
На рисунке, помимо точки касания, есть еще 2 точки. Спасибо авторам задания за них. Благодаря этим точкам, которые назовем А и С, мы моментально можем провести две прямые, параллельные осям. Они пересекутся в точке B.
Видишь треугольник АВС? Он прямоугольный.
∠АСВ будет равен ∠β (соответственные углы при параллельных прямых Ох и ВС секущей АС).
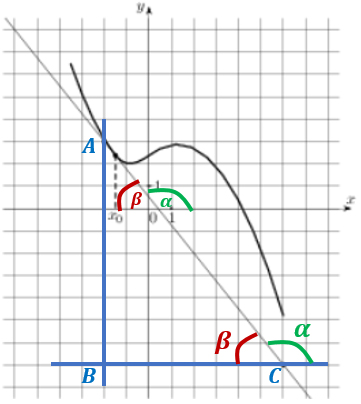
Найдем тангенс угла β. Он равен отношению противолежащего катета АВ к прилежащему катету ВС:
tgβ = AB/BC = 10/8 = 1,25.
Тангенсы смежных углов имеют противоположные значения, значит
tgβ = -tgα.
Если tgβ = 1,25, то tgα = -1,25.
Ответ: -1,25.