Последние решения
В фирме "Свежесть" стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле С=8500+6800n, где n - число колец, установленных в колодце. Пользуясь этой формулой, рассчитайте стоимость колодца из 6 колец. Ответ дайте в рублях.
#962
Найдите корень уравнения х+х/9=-10/3.
#961
Найдите значение выражения (√4а11·√9b4)/√a7b4 при а=7 и b=9.
#960
Найдите значение выражения (4/15)2-13/36.
#959
Найдите корень уравнения 3(2-x)+2x=3х-4.
#958
Найдите значение выражения ((a5)3 · a6)/a22 при a=2.
#957
Найдите значение выражения 10/49+(3/14)2.
#956
В амфитеатре 14 рядов, причем в каждом следующем ряду на одно и тоже число мест больше, чем в предыдущем. В пятом ряду 27 мест, а в восьмом ряду 36 мест. Сколько мест в последнем ряду амфитеатра?
#955
Площадь четырехугольника можно вычислить по формуле S=(d1d2sinα)/2, где d1 и d2 - длины диагоналей четырехугольника, α - угол между диагоналями. Пользуясь этой формулой, найдите длину d1, если d2=16, sinα=0,4, а S=12,8.
#954
Решите уравнение 2х2-1 7/25=0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
#953
У бабушки 20 чашек: 11 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
#952
Найдите значение выражения √(17·54)·√(17·22).
#951
Найдите значение выражения 5/12-8/15+1/6.
#950
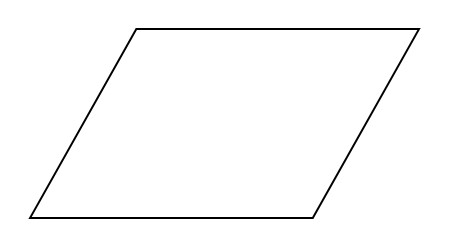
Один из углов параллелограмма равен 61°. Найдите больший угол параллелограмма. Ответ дайте в градусах.
#949
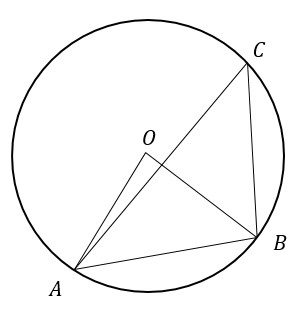
Треугольник АВС вписан в окружность с центром в точке О. Точки О и С лежат в одной полуплоскости относительно прямой АВ. Найдите угол АСВ, если угол АОВ равен 33°. Ответ дайте в градусах.
#948