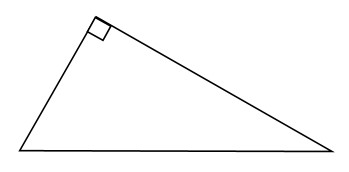
В прямоугольном треугольнике катет и гипотенуза равны 9 и 41 соответственно. Найдите другой катет этого треугольника.
#947
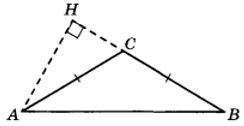
В тупоугольном треугольнике АВС известно, что АС = ВС = 10, высота АН равна √51 . Найдите косинус угла АСВ.
#936
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=17, AC=51, NC=32.
#905
В треугольнике ABC с тупым углом ACB проведены высоты AA1 и BB1. Докажите, что треугольники A1CB1 и ACB подобны.
#904
Катет и гипотенуза прямоугольного треугольника равны 20 и 52. Найдите высоту, проведенную к гипотенузе.
#883
Отрезки АВ и DC лежат на параллельных прямых, а отрезки АС и BD пересекаются в точке М. Найдите МС, если АВ=16, DC=24, AC=25.
#879
Прямая пересекает стороны АВ и ВС треугольника АВС в точках К и N соответственно. Известно, что АВ=12, ВС=15, АС=24, АК=7, CN=11. Найдите длину отрезка KN.
#849
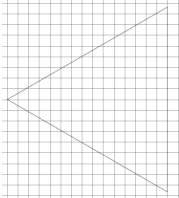
На клетчатой бумаге с размером клетки 1 × 1 изображён равносторонний треугольник. Найдите: а) радиус описанной около него окружности; б) радиус вписанной в него окружности.
#797
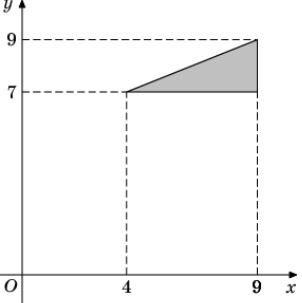
Найдите площадь треугольника, вершины которого имеют координаты (4;7), (9;7), (9;9).
#794
Найдите площадь треугольника, изображенного на рисунке.
#792
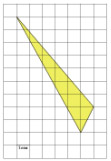
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. Ответ дайте в квадратных сантиметрах.
#791
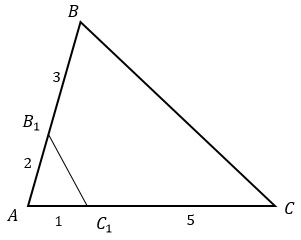
На сторонах АВ и АС треугольника АВС отмечены точки В1 и С1 соответственно. Найдите площадь треугольника АВ1С1, если АВ=5, ВВ1=3, АС1=1, СС1=5 и площадь четырехугольника ВСС1В1 равна 14.
#775
Точка Н является основанием высоты, проведенной из вершины прямого угла В треугольника АВС к гипотенузе АС. Найдите АВ, если АН = 4, АС = 16.
#767
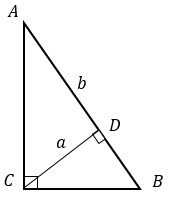
В прямоугольном треугольнике АВС проведена высота СD к гипотенузе АВ, СD = а, АD = b. Найдите: 1) ВС; 2) радиус окружности, вписанной в треугольник АВС; 3) отношение площадей треугольников АDС и АСВ.
#761
Найдите площадь правильного треугольника, сторона которого равна стороне ромба с диагоналями 10 и 12.
#758