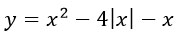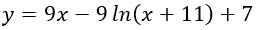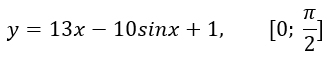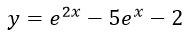На рисунке изображен график y=f'(x) – производной функции f(x) , определенной на интервале (−9; 3). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y=2x-19 или совпадает с ней.

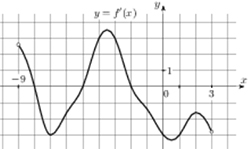
Геометрический смысл производной гласит, что производная функции равна углу наклона касательной к графику этой функции, т.е. f'(x) = k.

Угловой коэффициент прямой y = 2x - 19 равен 2 (k = 2).

А т.к. касательная параллельна этой прямой или совпадает с ней, то коэффициент у нее будет тот же.

И значение производной так же будет равно 2 (по геометрическому смыслу).

Дочертим на рисунке линию f'(x) = 2 и посчитаем точки, в которых значение производной равно 2.

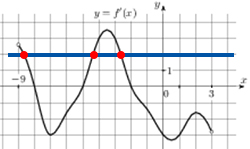
Ответ: 3.