Решите задачи:

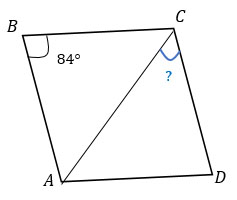
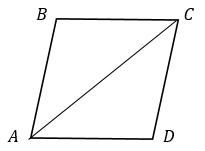
1. В параллелограмме ABCD проведена диагональ BD. Найдите сторону AD параллелограмма, если АВ = 6√2, ∠ADB = 30°, ∠BDC = 45°.

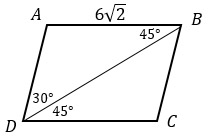
∠BDC = ∠ABD = 45° (накрест лежащие углы при пересечении параллельных прямых AB и CD секущей BD)

Рассмотрим треугольник ABD и воспользуемся теоремой синусов:

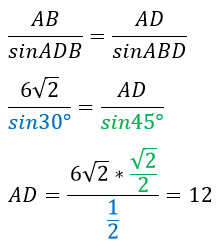
Ответ: 12.

2. Биссектриса одного из углов параллелограмма делит его сторону на отрезки 10 и 14.

а) Найдите периметр параллелограмма.

б) Найдите площадь параллелограмма, если большая его высота равна 6.

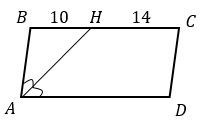
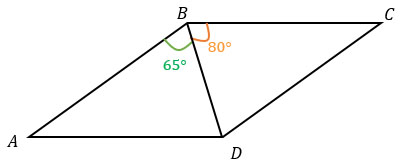
∠BHA = ∠HAD как накрест лежащие углы при пересечении параллельных прямых ВС и AD секущей АН. При этом ∠ВАН = ∠HAD, т.к. АН - биссектриса. Следовательно, ∠ВАН = ∠BHA и Δ ABH - равнобедренный со сторонами АВ = ВН = 10.

а) Периметр - это сумма длин всех сторон. В нашем случае для нахождения периметра параллелограмма воспользуемся формулой

Р = (АВ + ВС) · 2 = (10 + 24) · 2 = 68.

б) По логике бóльшая высота параллелограмма будет опущена на сторону АВ, значит, чтобы найти его площадь надо основание умножить на высоту, проведенную к нему, т.е.

S = АВ · h = 10 · 6 = 60.

Ответ: Р = 68, S = 60.

3. Стороны параллелограмма равны 3√3 и 2, а угол между ними равен 30°.

а) Найдите длину меньшей диагонали.

б) Найдите длину большей диагонали.

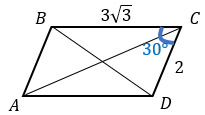
Если угол С равен 30°, то угол D будет равен 150°, т.к. эти углы являются односторонними при параллельных прямых. Из этого следует, что диагональ BD будет меньше диагонали АС, т.к. она лежит напротив меньшего угла.

а) По теореме косинусов выразим BD:

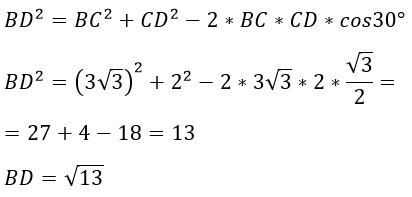
б) Т.к. ABCD - параллелограмм, то его противоположные стороны равны, следовательно, АD = BC = 3√3.

По теореме косинусов выразим АС:

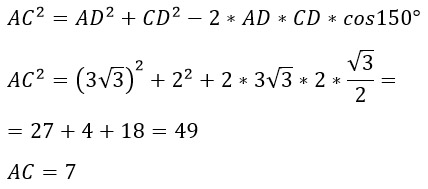
*соs150° я нашла по формуле приведения. Формула, кстати, выглядит так:

cos(180° - α) = -cosα

Для нашего значения: cos150° = cos(180° - 30°) = -cos30° = -√3/2

Ответ: 7.