Цилиндр и конус имеют общие основания и высоту. Объем цилиндра равен 72. Найдите объем конуса.
#967
Средняя линия трапеции равна 30. Одна из диагоналей трапеции делит среднюю линию в отношении 5:3. Найдите меньшее основание трапеции.
#966
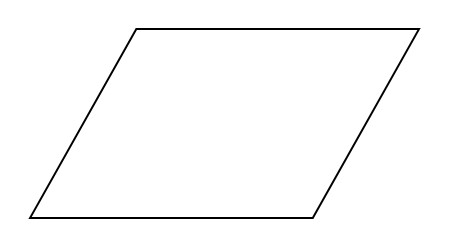
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. найдите длину ее средней линии.
#963
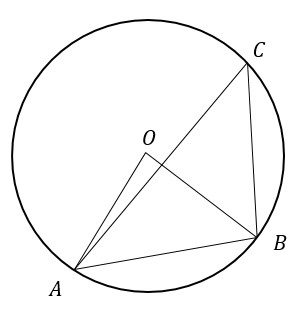
Один из углов параллелограмма равен 61°. Найдите больший угол параллелограмма. Ответ дайте в градусах.
#949
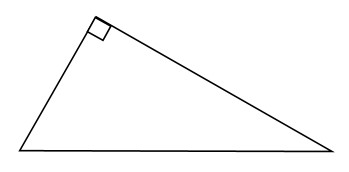
Треугольник АВС вписан в окружность с центром в точке О. Точки О и С лежат в одной полуплоскости относительно прямой АВ. Найдите угол АСВ, если угол АОВ равен 33°. Ответ дайте в градусах.
#948
В прямоугольном треугольнике катет и гипотенуза равны 9 и 41 соответственно. Найдите другой катет этого треугольника.
#947
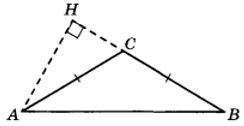
В тупоугольном треугольнике АВС известно, что АС = ВС = 10, высота АН равна √51 . Найдите косинус угла АСВ.
#936
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.
#906
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=17, AC=51, NC=32.
#905
В треугольнике ABC с тупым углом ACB проведены высоты AA1 и BB1. Докажите, что треугольники A1CB1 и ACB подобны.
#904
Катет и гипотенуза прямоугольного треугольника равны 20 и 52. Найдите высоту, проведенную к гипотенузе.
#883
В выпуклом четырехугольнике ABCD углы ABD и ACD равны. Докажите, что углы DAC и DBC также равны.
#882
Биссектрисы углов C и D трапеции ABCD пересекаются в точке Р, лежащей на стороне АВ. Докажите, что точка P равноудалена от прямых ВС, CD и AD.
#881
Через точку О пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны ВС и AD в точках К и М соответственно. Докажите, что ВК=DM.
#880
Отрезки АВ и DC лежат на параллельных прямых, а отрезки АС и BD пересекаются в точке М. Найдите МС, если АВ=16, DC=24, AC=25.
#879
