Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.

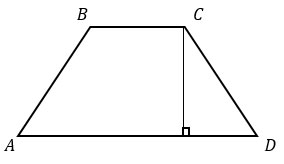
1) Проведем высоты ВЕ = СН.

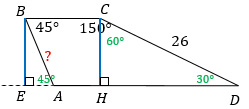
2) Рассмотрим треугольник CHD.

Т.к. ∠BCD = 150°, а ∠BCH = 90°, то ∠HCD = 150° – 90° = 60°, а ∠D = 90° – 60° = 30° (сумма острых углов прямоугольного треугольника равна 90).

Напротив угла в 30° лежит катет, длина которого в два раза меньше гипотенузы, значит СН = 26 : 2 = 13 = ВЕ (также можно найти длины высот через косинус ∠HCD).

3) ∠СBA = ∠BAE = 45° как накрест лежащие углы при пересечении параллельных прямых ВС и AD секущей АВ.

4) Рассмотрим треугольник ВЕА: ВЕ = 13, ∠BAE = 45°, значит

Ответ: 13√2