В равнобедренной трапеции ABCD с бОльшим основанием AD биссектриса угла А пересекается с биссектрисой угла С в точке F, а также пересекает сторону CD в точке К. Известно, что угол AFC равен 150°. Найдите FK, если CF=12√3.

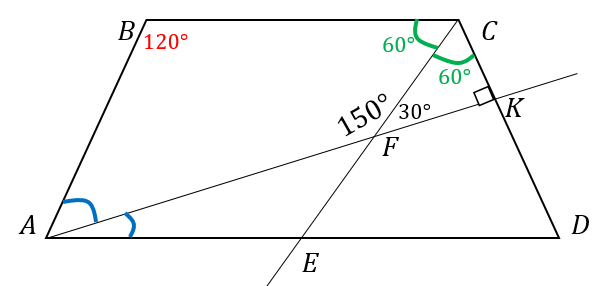
Т.к. биссектрисы АК и CE делят углы A и С пополам, то обозначим на чертеже равные углы одинаковыми цветами.

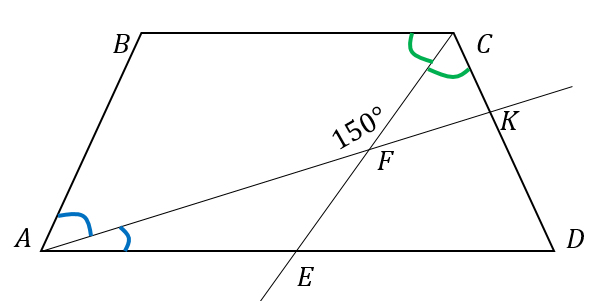
1) ∠А + ∠В = 180° – односторонние углы при пересечении параллельных прямых ВС и AD секущей АВ.

Т.к. трапеция равнобедренная, то ∠А + ∠С = 180°.

2) Т.к. АК и СЕ – биссектрисы, то сумма половинок углов А и С будет равна 90. Как это расписать?

∠А + ∠С = 180°

∠BAF + ∠FAE + ∠BCF + ∠FCK = 180°

2∠BAF + 2∠BCF = 180°     / :2

∠BAF + ∠BCF = 90°

3) В четырехугольнике ABCF сумма углов равна 360. Найдем угол В:

∠В = 360° – (∠BAF + ∠BCF + ∠AFC) = 360° – (90° + 150°) = 120°.

Т.к. трапеция равнобедренная, то ∠С = 120° тоже, а значит ∠BCF = ∠FCK = 60° (CF - биссектриса).

4) Рассмотрим треугольник CFK.

∠FCK = 60°, ∠СFK = 180° – 150° = 30° (углы AFC и CFK – смежные), следовательно, ∠CKF = 90°, т.е. треугольник CFK – прямоугольный.

5) Найдем FK.

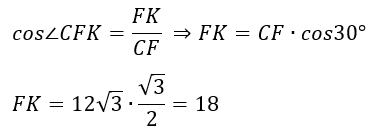
Ответ: 18.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.