В равнобедренную трапецию, периметр которой равен 40, а площадь равна 80, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до ее меньшего расстояния.

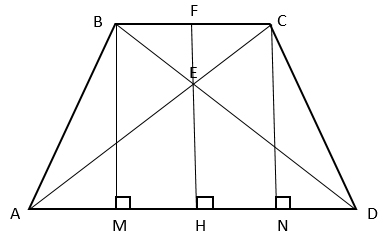
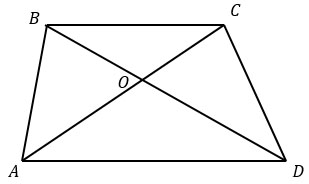
Пусть диагонали трапеции пересекаются в точке Е. Через эту точку проведем высоту трапеции FH.

Тот факт, что в трапецию можно вписать окружность, говорит о том, что суммы противоположных сторон трапеции равны, т.е.

AB + CD = BC + AD, причем АВ = CD (трапеция равнобедренная), значит,

2АВ = BC + AD (пойдет в систему).

Если периметр трапеции равен 40, то суммы противоположных сторон будут равны 20, следовательно,

2АВ = 20;

АВ = 10.

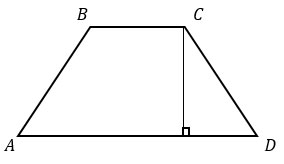
Запишем формулу для нахождения площади трапеции и найдем FH - высоту трапеции.

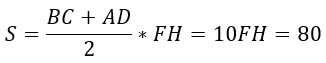
Отсюда, FH = 8.

Рассмотрим прямоугольный треугольник ABM. По теореме Пифагора найдем АМ.

АМ² = АВ² - ВМ² = 100 - 64 = 36;

АМ = 6.

Дополнительно проведем высоты BM и CN. Они, как и FH, равны 8.

Т.к. трапеция равнобедренная, то ВС = MN, AM = ND и имеет место равенство

AD = AM + MN + ND;

AD = AM + BC + AM;

AD - BC = 2AM = 2 · 6 = 12 (пойдет в систему).

Составим систему уравнений.

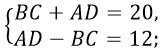
Воспользуемся методом сложения неравенств, тогда система примет вид:

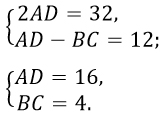
Треугольники BEC и AED подобны по двум углам, т.к. ∠ВЕС = ∠AED (вертикальные) и ∠CBD = ∠EDA (накрест лежащие при пересечении параллельных прямых ВС и AD секущей BD).

Из подобия треугольников следует пропорциональность сторон и, в данном случае, высот, тогда

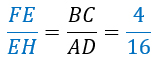
Выразим EH через FE и FH = 8.

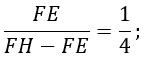
Найдем FE.

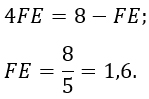
Ответ: 1,6.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.