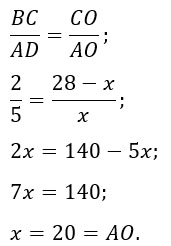ТОП 15 примеров из раздела "Трапеция"
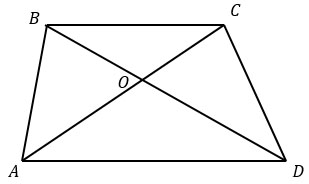
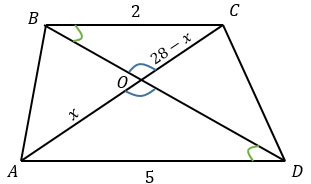
Диагонали АС и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC = 2, AD = 5, AC = 28. Найдите AO.
#486
Сумма двух углов равнобедренной трапеции равна 220°. Найдите меньший угол трапеции. Ответ дайте в градусах.
#472
В равнобедренной трапеции ABCD с бОльшим основанием AD биссектриса угла А пересекается с биссектрисой угла С в точке F, а также пересекает сторону CD в точке К. Известно, что угол AFC равен 150°. Найдите FK, если CF=12√3.
#876
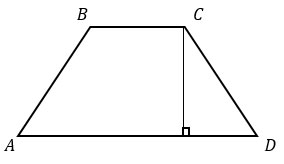
Высота равнобедренной трапеции, проведенная из вершины С, делит основание AD на отрезки длиной 11 и 14. Найдите длину основания ВС.
#464
Найдите площадь трапеции, изображенной на рисунке.
#488
В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке Р. Докажите, что площади треугольников АРВ и CPD равны.
#727
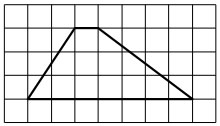
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.
#355
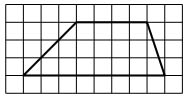
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.
#520
Биссектрисы углов C и D трапеции ABCD пересекаются в точке Р, лежащей на стороне АВ. Докажите, что точка P равноудалена от прямых ВС, CD и AD.
#881
В трапецию, сумма длин боковых сторон которой равна 24, вписана окружность. Найдите длину средней линии трапеции.
#371
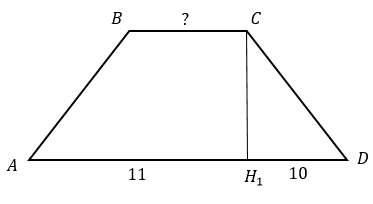
Высота равнобедренной трапеции проведенная из вершины C делит основание AD на отрезки, длиной 10 и 11. Найдите длину основания BC.
#595
Около трапеции, один из углов которой равен 44°, описана окружность. Найдите остальные углы трапеции.
#372
В трапеции ABCD известно, что AB = CD, ∠BDA = 67° и ∠BDC = 28°. Найдите угол ABD. Ответ дайте в градусах.
#469
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.
#906
В равнобедренную трапецию, периметр которой равен 40, а площадь равна 80, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до ее меньшего расстояния.
#701