Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 18, а одна из диагоналей равна 72. Найдите углы ромба.

Пусть дан ромб ABCD с диагоналями, которые пересекаются в точке О.

Расстояние от точки до прямой – это перпендикуляр, значит, ОН – высота треугольника АОD, которая равна 18.

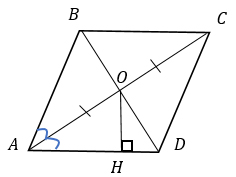
Что мы знаем о ромбе?

То, что диагонали точкой пересечения делятся пополам и то, что диагонали являются биссектрисами углов. Что ж, используем эту информацию, чтобы решить эту задачу.

Сразу можно найти длину отрезков АО и ОС:

АО = ОС = 72 : 2 = 36.

Рассмотрим треугольник АОН. Он прямоугольный. Выразим синус угла ОАН.

Синус – это отношение противолежащего катета к гипотенузе, значит

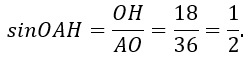
Из этого следует, что ∠ОАН = 30°. 

А ∠А в два раза больше ∠ОАН, т.е. ∠А = 60° (т.к. диагонали ромба делят угол пополам; это оговаривалось выше).

Углы А и В – односторонние при пересечении параллельных прямых ВС и АD секущей АВ, следовательно ∠В = 180° – ∠А = 180° - 60° = 120°.

Помимо этого у ромба противоположные углы равны, значит, ∠А = ∠С = 60° и ∠В = ∠D = 120°.

Ответ: 60°, 60°, 120°, 120°.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.