В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC = ED. Докажите, что данный параллелограмм — прямоугольник.

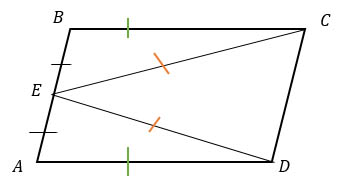
Рассмотрим треугольники ВЕС и АЕD:

1) ВЕ = АЕ (т.к. Е - середина АВ);

2) ЕС = ЕD (по условию);

3) ВС = AD (т.к. противоположные стороны параллелограмма равны).

Значит, ΔВЕС = ΔAED по трем сторонам.

Из равенства треугольников следует, что ∠В = ∠А.

Углы В и А - односторонние углы при пересечении параллельных прямых ВС и AD секущей АВ, следовательно их сумма равна 180°, т.е. ∠В = ∠А = 90°.

Если в параллелограмме хотя бы один угол равен 90°, то этот параллелограмм является прямоугольником.

Что и требовалось доказать.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.