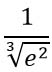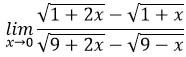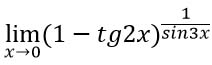Найдите предел функции (1-tg2x)^(1/sin3x) при х стремящемся к 0.

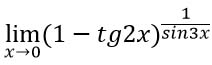
Заменим вычитание на сложение с отрицательным числом.

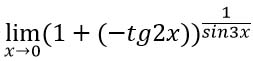
Преобразуем выражение таким образом, чтобы можно было воспользоваться вторым замечательным пределом по формуле . В данном примере α = -tg2x, значит в степени надо организовать  Для этого возводим (1+(-tg2x)) в нужную нам степень  И чтобы исходная степень не изменилась, умножаем ее на –tg2x.

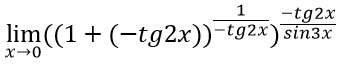
Абракадабра  превращается в прекрасную букву e, а сам предел перемещается в степень.

________________

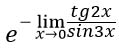
Разбираемся со степенью. Подставляя 0 вместо иксов получаем неопределенность вида 0/0. Воспользуемся правилом Лопиталя: найдем производные отдельно от числителя и отдельно от знаменателя.

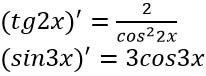
Сразу заменяем деление на 3cos3x умножением на дробь.

________________

Итак, что же получается...

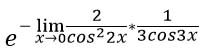
Подставляем 0 вместо иксов. Считаем. Получается 2/3.

Избавимся от отрицательной степени.

Можно оставить ответ и с дробной степенью, а можно записать и через корень. Как душа пожелает)