Через точку О пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны ВС и AD в точках К и М соответственно. Докажите, что ВК=DM.

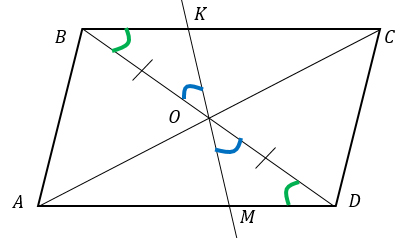
Рассмотрим треугольники ВКО и MDO:

1) ∠KBO = ∠ODM - накрест лежащие углы при пересечении параллельных прямых ВС и AD секущей BD.

2) ∠BOK = ∠MOD - вертикальные.

3) ВО = ОD, т.к. диагонали параллелограмма точкой пересечения делятся пополам.

Отсюда следует, что треугольники ВКО и MDO равны по стороне и двум прилежащим к ней углам.

А из равенства треугольника следует равенство их соответствующих элементов, т.е.  ВК = MD.

Что и требовалось доказать.