Биссектриса угла М параллелограмма МРКС пересекает сторону РК в точке В. Найдите периметр параллелограмма, если МР = 14, ВК = 15 см.

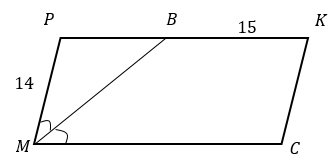
Докажем, что ΔМРВ - равнобедренный.

Т.к. МВ - биссектриса, то ∠РМВ = ∠ВМС.

∠РВМ = ∠ВМС как накрест лежащие углы при пересечении параллельных прямых РК и МС секущей МВ.

Значит, ∠РМВ = ∠РВМ и ΔМРВ - равнобедренный (т.к. ∠РМВ = ∠РВМ - углы при основании).

Если ΔМРВ равнобедренный, то МР = РВ = 14.

Найдем РК: РК = РВ + ВК = 14 + 15 = 29.

Найдем периметр: Р = (МР + РК) · 2 = (14 + 29) · 2 = 43 · 2 = 86 см.

Ответ: 86 см.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.