Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К. а) Докажите, что треугольник BKA равнобедренный. б) Найдите периметр параллелограмма, если ВК=4, СК=19.

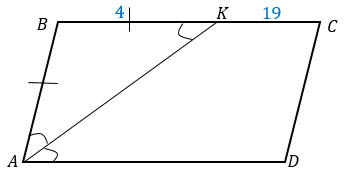
а) Если АК - биссектриса, то ∠ВАК = ∠KAD.

∠KAD = ∠BKA как накрест лежащие углы при параллельных прямых BC и AD секущей АК.

Следовательно, ∠ВАК = ∠ВКА - углы при основании ΔВКА и ΔВКА - равнобедренный.

Что и требовалось доказать.

б) Т.к. ΔВКА - равнобедренный, то АВ = ВК.

Формула для нахождения периметра параллелограмма: Р = 2АВ + 2ВС = 2ВК + 2(ВК + КС) = 2 · 4 + 2(4 + 19) = 8 + 46 = 54.

Ответ: 54.