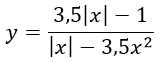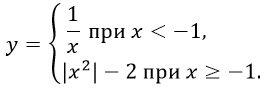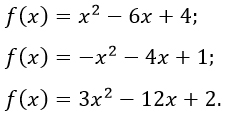-
Решения
-
Теория
-
Задачник
-
Идеи для учителя
- Заказать обучение
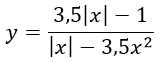
x = 0 – критическая точка, в ней подмодульное выражение меняет знак. Поэтому будем рассматривать два случая: когда x > 0 и x < 0.
1) При x > 0 функция примет такой вид
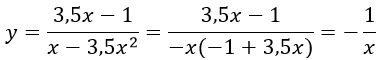
Графиком данной функции будет гипербола, к тому же, сразу определимся с ОДЗ. Т.к. у нас дана дробь, то ее знаменатель не может равняться нулю. Поэтому, икс не должен равняться 0 и 2/7 (х ≠ 0 и х ≠ 2/7).
Сразу найдем координаты точек, по которым будем чертить график.
| х | 0,5 | 1 | 2 |
| у | -2 | -1 | -0,5 |
Найдем координаты выколотой точки: если x ≠ 2/7, то y ≠ -3,5.
2) При х < 0 функция примет вид
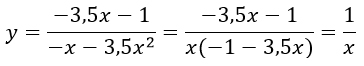
ОДЗ: х ≠ 0 и х ≠ -2/7.
Найдем координаты точек.
| х | -0,5 | -1 | -2 |
| у | -2 | -1 | -0,5 |
Найдем координаты выколотой точки: если x ≠ -2/7, то y ≠ -3,5.
3) Теперь можно чертить график (синие кусочки гипербол).
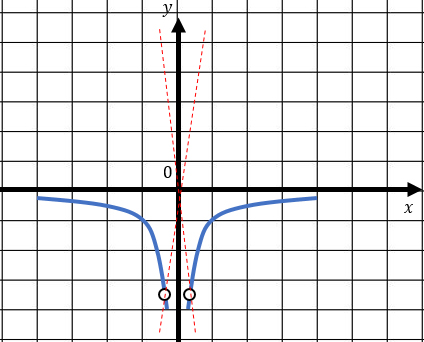
y = kx – прямая, проходящая под наклоном через начало координат (k – угловой коэффициент). И есть две потенциальные прямые, которые с нашим графиком не имеют общих точек (на координатной плоскости они отмечены красным цветом). Осталось лишь найти чему равен коэффициент k.
Обе прямые непременно должны проходить через выколотые точки. И логично предположить, что чтобы найти k надо в уравнение y = kx подставить координаты этих выколотых точек. Это мы сейчас и сделаем.
Для точки (-2/7; -3,5)
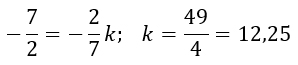
Для точки (2/7; -3,5)
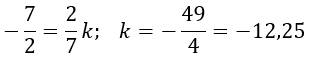
И не стоит забывать, что при k = 0 прямая y = kx превращается в прямую y = 0, которая совпадает с осью Ох. А, как известно, гипербола ее никогда не пересечет.
Ответ: при k = ±12,25 и k = 0 прямая y = kx не имеет с графиком общих точек.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.