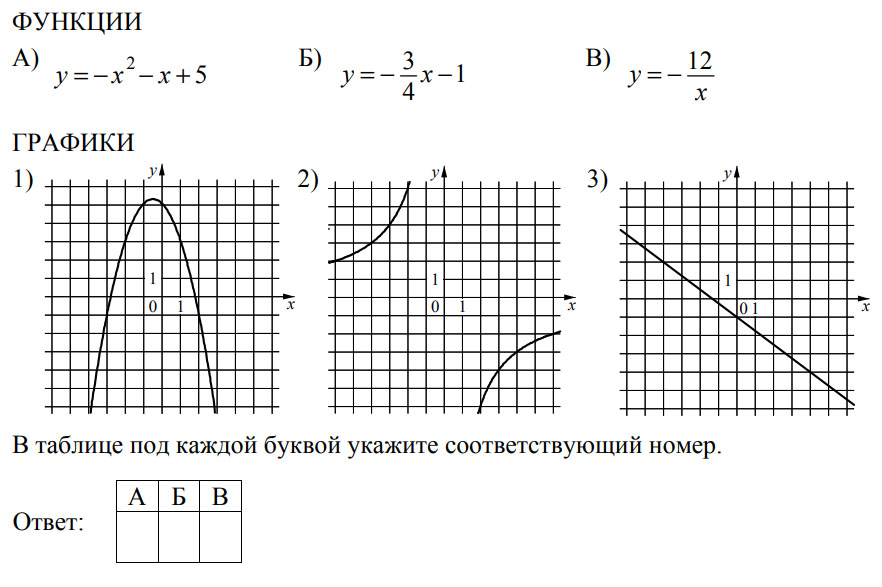
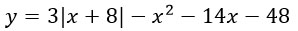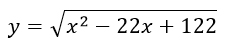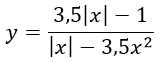-
Решения
-
Теория
-
Задачник
-
Идеи для учителя
- Заказать обучение
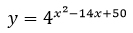
Для нахождения первой производной данной функции будем ориентироваться на следующую табличную производную:
(ах)' = axlna.
И не забываем, что функция сложная.
y' = 4x^2 - 14x + 50 · ln4 · (x2-14x+50)' = 4x^2 - 14x + 50 · ln4 · (2x -14).
Приравняем производную к 0:
4x^2 - 14x + 50 · ln4 · (2x -14) = 0.
Произведение равно 0 тогда и только тогда, когда один из множителей равен 0, т.е.
4x^2 - 14x + 50 = 0 или 2x -14 = 0
корней нет х = 7
Т.к. мы находим наименьшее значение функции, то найденный корень подставляем вместо икса в функцию.
y(7) = 47^2 - 14 · 7 + 50 = 41 = 4.
Ответ: 4.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.