Окружности с центрами в точках P и Q не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении a : b. Докажите, что диаметры этих окружностей относятся как a : b.

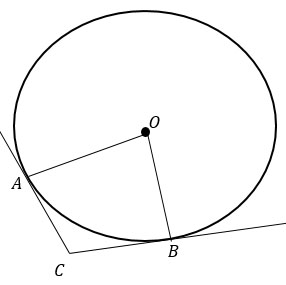
Проведем радиусы РР₁ и QQ₁ в точки касания. Получили два прямоугольных треугольника РР₁О и QQ₁O (радиус, проведенный в точку касания, перпендикулярен касательной).

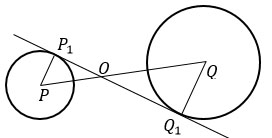
Треугольники РР₁О и QQ₁O подобны по двум углам, т.к. ∠РР₁О = ∠QQ₁О = 90° и ∠Р₁ОР = ∠Q₁OQ - вертикальные.

Из подобия треугольников следует пропорциональность их сторон:

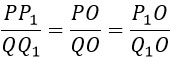
Это значит, что если , то   (1).

Т.к. радиус - это половина диаметра, то   и  .

Произведем замену в формуле (1):

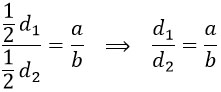
Что и требовалось доказать.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.