Радиус вписанной в квадрат окружности равен 6√2. Найдите радиус окружности, описанной около этого квадрата.

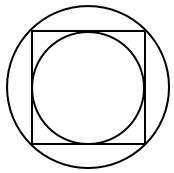
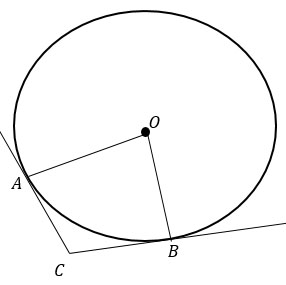
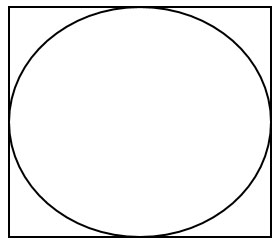
Проведем радиусы АО и ОВ вписанной и описанной окружностей.

Стороны квадрата являются касательными к вписанной окружности, а радиус, проведенный в точку касания, перпендикулярен касательной, т.е. угол ОАВ - прямой и треугольник ОАВ - прямоугольный.

Кроме того, точка А делит сторону квадрата пополам и радиус вписанной окружности равен половине стороны квадрата, т.е. АВ = АО = 6√2.

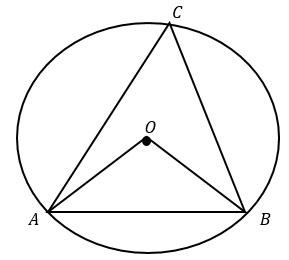
В данном случае тот факт, что А - середина стороны очевиден и это задание, встречающееся в 1-ой части ОГЭ по математике, не требует доказательства. Но если доказательство все-таки необходимо, то надо провести еще один радиус ОС описанной вокруг квадрата окружности /точку С поставить в левом верхнем углу квадрата/ и доказать равенство отрезков АВ и АС через равенство треугольников АОВ и АОС.

По теореме Пифагора найдем ОВ.

ОВ² = ОА² + АВ²;

ОВ² = (6√2)² + (6√2)² = 36 · 2 + 36 · 2 = 144;

ОВ = √144 = 12.

Ответ: 12.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.