Точка К – середина боковой стороны СD трапеции ABCD. Докажите, что площадь треугольника КАВ равна половине площади трапеции.

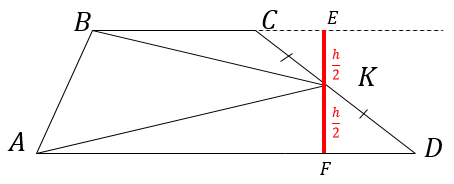
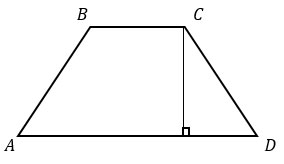
Красный отрезок EF (в дальнейшем будем его обозначать просто h) – это высота трапеции, которая состоит из двух высота двух треугольников BCK и AKD, причем эти высоты будут равны, т.к. K – середина CD.

Доказывается очень просто: рассматриваем прямоугольные треугольники СЕК и FKD.

Углы ECK и KDF равны как накрест лежащие при пересечении параллельных прямых ВС и АD секущей СD. Также по условию задачи CK = KD. Это значит, что треугольники СЕК и FKD равны по гипотенузе и острому углу, следовательно, EK = KF=h/2.

Приступим к основной проблеме)

Если площадь трапеции равна

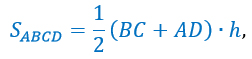
то половина площади трапеции будет равна

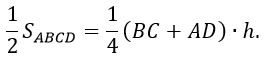
Наша задача: доказать, что 

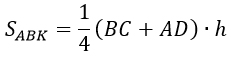
Выразим площади треугольников BCK и AKD:

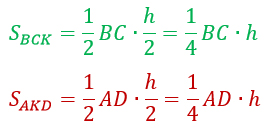
Чтобы найти площадь треугольника АВК надо из площади трапеции вычесть площади двух других треугольников:

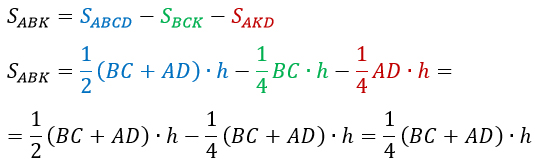
Что и требовалось доказать.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.