-
Решения
-
Теория
-
Задачник
-
Идеи для учителя
- Заказать обучение
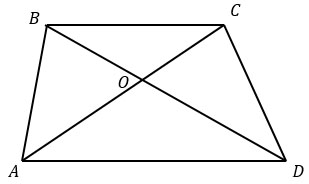
По условию задачи AC = 7, BD = 15, MN = 10.
Чтобы найти площадь трапеции надо среднюю линию умножить на высоту. Средняя линия известна, значит задача сводится к нахождению высоты трапеции.
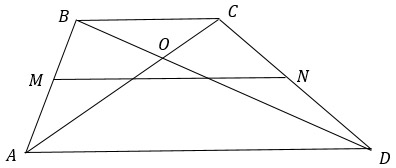
Есть несколько формул для нахождения высоты через диагонали, но они несколько сложноваты для запоминания и совсем не очевидны. Поэтому пойдем окольными путями и сделаем дополнительное построение.
Проведем отрезок СЕ, параллельный диагонали BD. Получим четырехугольник BCED.
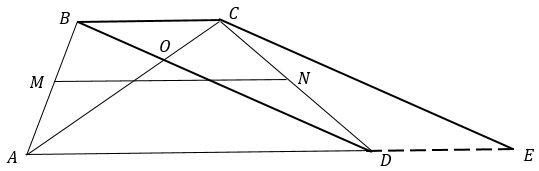
BCED - параллелограмм, т.к. СЕ || BD и ВС || DE (DE лежит на продолжении стороны AD, которая параллельна ВС из определения трапеции), значит, СЕ = BD = 15.
Рассмотрим треугольник АСЕ: АС = 7, СЕ = 15, АЕ = AD + DE = AD + BC. Если полусумма оснований равна средней линии, то просто сумма оснований будет равна удвоенной средней линии, значит АЕ = 2MN = 20.
Найдем площадь треугольника ACE по формуле Герона:
![]()
p - это полупериметр, р = (15 + 7 + 20)/2 = 21.
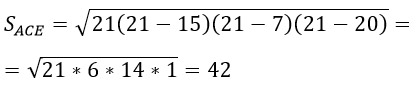
Площадь треугольника ACE также можно найти и через высоту, а она нам ох как нужна, потому что высота трапеции и высота треугольника ACE, проведенные к нижнему основанию, равны между собой:
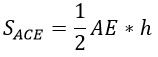
Найдем h.
½ · 20 · h = 42;
h = 4,2.
Найдем площадь трапеции.
SABCD = MN · h = 10 · 4,2 = 42.
Ответ: 42.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.