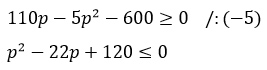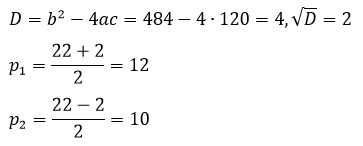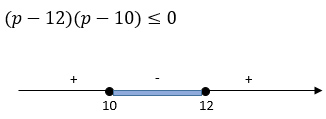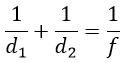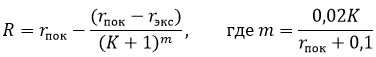Зависимость объема спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены p (тыс. руб. за единицу) задается формулой q=110-5p. Выручка предприятия r (в тыс. руб. за месяц) вычисляется по формуле r(p)=qp. Определите наибольшую цену p, при которой месячная выручка r(p) составит не менее 600 тыс. рублей. Ответ приведите в тыс. руб. за единицу.

Энергия заряженного конденсатора W в джоулях (Дж) вычисляется по формуле W=(CU^2)/2, где С - емкость конденсатора в фарадах (Ф), а U - разность потенциалов на обкладках конденсатора в вольтах (В). Найдите энергию конденсатора (в Дж) емкостью 10^(-4) Ф, если разность потенциалов на обкладках конденсатора равна 40 В.

Материальная точка движется прямолинейно по закону x(t)=t^2-3t-29 , где x – расстояние от точки отсчета в метрах, t – время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3 с.

Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f=28 см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 40 до 60 см, а расстояние d2 от линзы до экрана - в пределах от 53 до 77 см. Изображение на экране будет четким, если выполнено соотношение 1/d1 + 1/d2 = 1/f. Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы ее изображение на экране было четким. Ответ дайте в сантиметрах.

Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой tF=1,8tC+32, где tС - градусы Цельсия, tF - градусы Фаренгейта. Какая температура по шкале Фаренгейта соответствует -25º градусов по шкале Цельсия?

Рейтинг R интернет-магазина вычисляется по формуле R=r_пок-(r_пок-r_экс)/(K+1)^m , где m=0,02K/(r_пок+0,1), r_пок – средняя оценка магазина покупателями, r_экс – оценка магазина, данная экспертами, К – число покупателей, оценивших магазин. Найдите рейтинг интернет-магазина, если число покупателей, оценивших магазин, равно 7, их средняя оценка равна 0,32, а оценка экспертов равна 0,22.

Формула кинетической энергии тела E=(mv^2)/2. Найдите скорость тела с кинетической энергией 80 (кг*м^2)/с^2, если масса этого тела равна 10 кг.

Известно, что 1+2+3+...+n=n(n+1)/2. Найдите сумму 1+2+3+...+100.

Найдите m из равенства E=mgh, если g=9,8, h=4, E=50,96.

Площадь треугольника можно вычислить по формуле S=√p(p-a)(p-b)(p-c), где а, b, с – стороны треугольника, а p=(a+b+c)/2 - полупериметр треугольника. Пользуясь этой формулой, найдите площадь треугольника, если a = b = 50, с = 60.

Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой F=1,8C+32, где С - градусы Цельсия, F - градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 50º по шкале Фаренгейта?

Высота над землей подброшенного вверх мяча меняется по закону h(t) = 1,2 + 10t - 5t^2, где h – высота (в метрах), t – время (в секундах), прошедшее с момента броска. Сколько секунд мяч будет находится на высоте не менее 3 метров?

Мощность обогревателя (в ваттах) можно вычислить по формуле P=U^2/R, где U — напряжение в сети (в вольтах), R — сопротивление (в омах). Пользуясь этой формулой, найдите мощность обогревателя, включённого в сеть с напряжением 220 В, если сопротивление обогревателя равно 25 Ом. Ответ дайте в ваттах.

Среднее арифметическое трех чисел а, b, c вычисляется по формуле x=(a+b+c)/3. Вычислите среднее арифметическое чисел 4,1; 1/3; 2/3.

Чтобы найти плотность вещества, пользуются формулой ρ=m/V, где m – масса вещества, V – его объем. Найдите плотность вещества массой 4 кг, занимающего объем 1600 см^3. Ответ дайте в кг/м^3.

Некоторая компания продает свою продукцию по цене p=400 рублей за единицу, переменные затраты на производство одной единицы продукции составляют v=200 рублей, постоянные расходы предприятия f=500000 рублей в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле π(q)=q(p-v)-f. Определите месячный объем производства q (единиц продукции), при которой месячная операционная прибыль предприятия будет равна 300000 рублей.