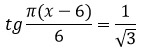Решите уравнение и в ответе запишите наибольший положительный корень: tg((pi(x-6))/6)=1/(sqrt3).

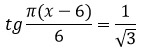
С помощью тригонометрического круга определимся: тангенс какого угла равен 1/√3?

По картинке видно, что нас интересует углы в 30° и 210°, а еще куча их братьев, которых мы получим, если будем эти углы "крутить" по окружности.

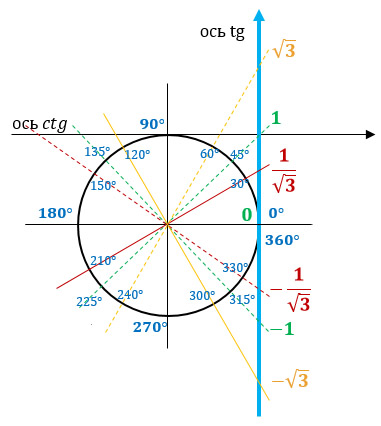
В обобщенном виде эти все углы надо записать так: π/6 + πk, где k ∈ Z.

Тогда исходное уравнение примет вид:

Умножим обе части уравнения на 6.

Перенесем известные в одну сторону, а неизвестные - в другую.

Обе части разделим на π.

Теперь найдем наименьший положительный корень. Для этого вместо k будем подставлять какие-нибудь целые числа.

Если k = 0, то х = 7.

Если k = 1, то х = 13.

Если k = -1, то х = 7.

Если k = -2, то х = -5.

Ответ: 7.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.