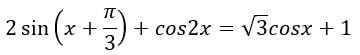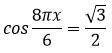-
Решения
-
Теория
-
Задачник
-
Идеи для учителя
- Заказать обучение
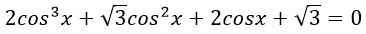
Чтобы решить это уравнение надо разложить его на множители. Выделю разными цветами то, что мы должны будем сгруппировать:
![]()
Из голубой пары слагаемых вынесем за скобку cos2x, а из зеленой - единицу, которая не пишется, потому что при умножении числа на 1 получается то же самое число.
![]()
Теперь выносим за скобку общий множитель "бордовую скобку". Получим такое уравнение:
![]()
Произведение равно 0 тогда, когда один из множителей равен 0.
Уравнение свелось к двум простейшим уравнениям, одно из которых корней не имеет потому, что квадрат не может быть отрицательным.
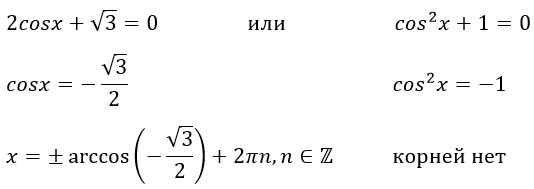
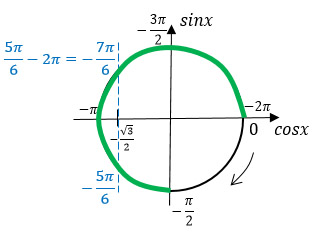
Наглядно изобразим, где у нас находятся корни уравнения и чему они равны:
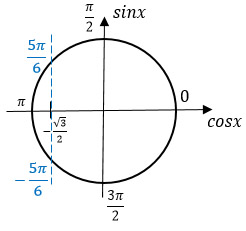
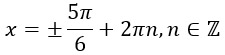
Как получить 5π/6? Из π вычесть π/6, т.к. cos(√3/2) = π/6.
Переходим ко второй части задания. Нужный промежуток я выделила зеленым цветом. Именно ему должны принадлежать какие-то корни.
Т.к. промежуток отрицательный, то и корни должны быть отрицательные.
От корня уравнения 5π/6 делаем один оборот по часовой стрелке и попадаем в корень -7π/6.
А корень -5π/6 и так подходит без каких-либо манипуляций.
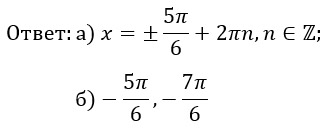
Как проверить правильность выбранных корней, если не до конца что-то понимаешь?
Просто откинь π и посчитай значение получившейся дроби.
Откинем пи у отрезка и получим такую абракадабру: [-2; -0,5]. Поменяем местами эти числа для нормального восприятия: [-0,5; -2].
Откинем пи у корня -5π/6: получим число -0,8.... Оно принадлежит промежутку [-0,5; -2]. Значит, корень -5π/6 ∈ [-2π; -π/2].
То же самое проделай с корнем -7π/6 и убедись, что он верный.
Сразу оговорюсь, что это не верное решение, а всего лишь небольшой лайфак)
Удачи!