Биссектрисы углов А и В при боковой стороне АВ трапеции ABCD пересекаются в точке F, а точка М - середина стороны АВ. а) Докажите, что MF=1/2AB; б) Найдите AF, если MF=6.5, BF=5.

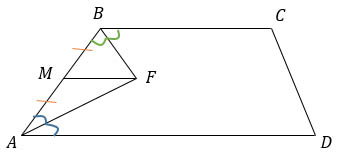
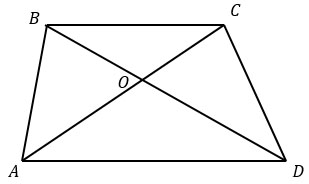
а) Углы А и В односторонние при пересечении параллельных прямых ВС и AD секущей АВ, т.е. ∠А + ∠В = 180°.

Т.к. AF и BF - биссектрисы, то ∠BAF + ∠ABF = 90°.

ΔABF - прямоугольный, т.к. ∠BFA = 180° - (∠BAF + ∠ABF) = 180° - 90° = 90°.

Т.к. АМ = МВ (по условию), значит MF - медиана, а медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы, т.е. MF = ½AB.

Что и требовалось доказать.

б) Из доказанного в пункте а): АВ = 2MF = 2 · 6.5 = 13.

По теореме Пифагора

Ответ: 12.