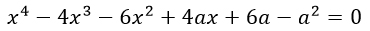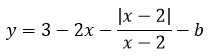Дана функция y=3-2x-|x-2|/(x-2)-b. Определите количество целых значений параметра b, при которых уравнение y=0 не имеет корней.

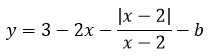
Сразу оговорим, что х ≠ 2, т.к. знаменательно не должен равняться 0.

Исследуем уравнение

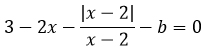
х = 2 – критическая точка. В ней модуль меняет знак. Рассмотрим два случая: когда x > 2 и когда х < 2.

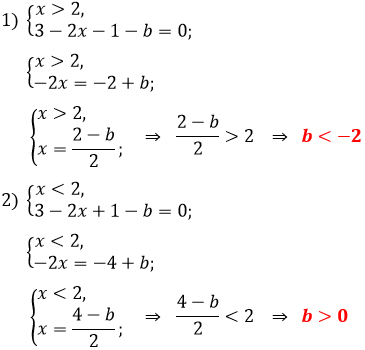
Исходное уравнение будет иметь корни при b ∈ (-∞; -2) ∪ (0; +∞).

А вот при b ∈ [-2; 0] уравнение корней иметь не будет.

Ответ: уравнение не имеет решений в ТРЁХ случаях: при b = -2, b = -1 и b = 0.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.