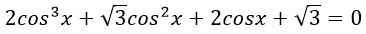Решите уравнение (x^2-4)^2+(x^2-3x-10)^2.

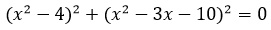
Разложим трехчлен во вторых скобках на множители. Для этого, используя теорему Виета, решим квадратное уравнение:

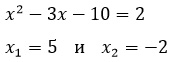
Разложение на множители будет выглядеть так:

Подставляем разложение в исходное уравнение:

Содержимое первых скобок разобьем на множители по формуле сокращенного умножения «Разность квадратов». И немножко преобразуем:

Вынесем общий множитель за скобку:

Произведение равно нулю тогда, когда один из множителей равен 0. Получаем два уравнения и решаем их:

Ответ: -2

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.