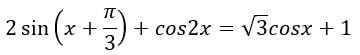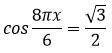а) Решите уравнение 2sin(x+пи/3)+cos2x=(sqrt3)cosx+1. б) Укажите корни этого уравнения, принадлежащие отрезку [-3пи; -3пи/2].

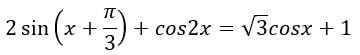
Для упрощения этого уравнения нам понадобятся две формулы:

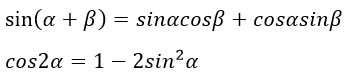
Делаем замену, согласно этим формулам, подсчитываем то, что возможно подсчитать.

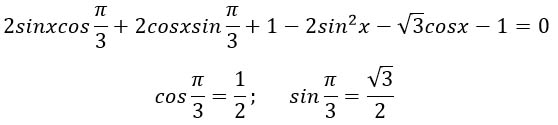
Приводим подобные слагаемые, выносим общий множитель за скобку.

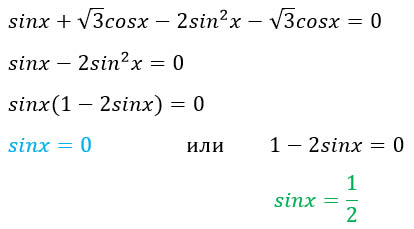
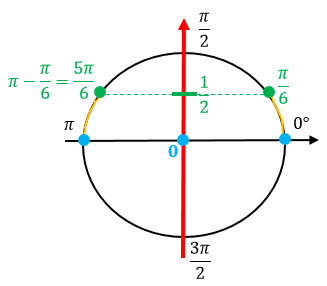
Отметим на тригонометрической окружности точки, в которых sinx = 0 и sinx = ½, не забывая при этом, что синус - это ордината (красная ось). Проведя линии, перпендикулярные оси ординат, мы упремся в 4 точки: 0, π, π/6 и 5π/6.

Это еще не ответ. По окружности эти точки могут "гулять" и менять свои значения в зависимости от количества оборотов по часовой стрелке и против часовой.

Голубые точки попадают друг в друга, если мы будем делать половину оборота по окружности, т.е. π. Точка π/6 будет попадать в себя после полного оборота окружности, т.е. 2π. То же самое с точкой 5π/6.

Исходя из этих данных, получим следующие корни уравнения:

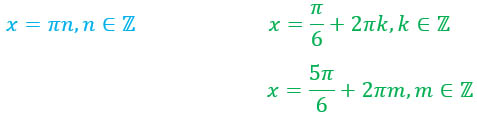
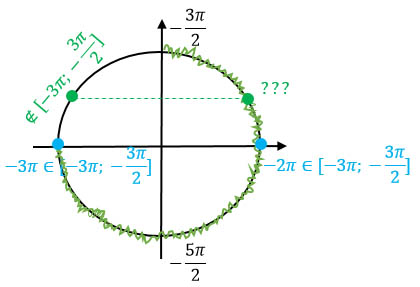
Теперь определим, какие конкретные корни, без всяких там оборотов, попадут в промежуток [-3π; -3π/2].

Сделать это очень просто по окружности. Начертим новую и отметим на ней, где будет находится нужный нам промежуток.

Невооруженным глазом видно,  что корни -2π и -3π нам подходят, а корень, который у нас шел под точкой 5π/6 вообще лежит не там, где надо, и рассматривать его не имеет смысла. Но какой же корень прячется под точкой, которая изначально была равна π/6?

Сделать это очень просто. Мы в эту точку попадаем, когда делаем 1 оборот против часовой стрелки, т.е. когда k = -1. Подставим это значение в общий корень уравнения x = π/6 + 2πk, k ∈ Z.

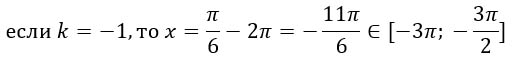
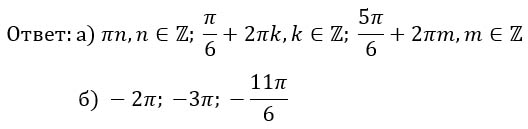
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.