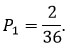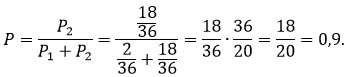ТОП 15 примеров из раздела "Теория вероятностей"
Первый игральный кубик обычный, а на гранях второго кубика нет нечетных чисел, а четные числа 2, 4 и 6 встречаются по два раза. В остальном кубики одинаковые. Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 4 и 6 очков. Какова вероятность того, что бросали первый кубик?
#930
Симметричную монету бросают 11 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?
#922
В небольшом магазине работают два продавца - Василий и Сергей. Каждый из них может быть занят с клиентом с вероятностью 0,4. При этом они могут быть заняты одновременно с вероятностью 0,3. Найдите вероятность того, что в случайно выбранный момент времени занят только Василий, а Сергей свободен.
#612
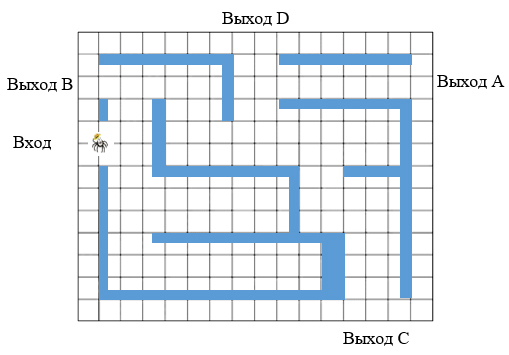
На рисунке изображен лабиринт. Паук заползает в лабиринт в точке "Вход". Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому еще не полз. Считая, что выбор дальнейшего пути чисто случайный, определите: а) с какой вероятностью паук придет к выходу D; б) с какой вероятностью паук придет к любому из выходов.
#631
Клиент получает в банке кредитную карту. Четыре последние цифры номера карты случайные. Какова вероятность того, что последние четыре цифры состоят из двух повторяющихся групп по 2 различные цифры, например 0404 или 5252?
#744
Стрелок в тире стреляет по мишени до тех пор, пока не поразит ее. Известно, что он попадает в цель с вероятностью 0,1 при каждом отдельном выстреле. Сколько патронов нужно дать стрелку, чтобы он поразил цель с вероятностью не менее 0,4?
#924
В городе 48% взрослого населения мужчины. Пенсионеры составляют 12,6% взрослого населения, причем доля пенсионеров среди женщин равна 15%. Для проведения исследования социологи случайным образом выбрали взрослого мужчину, проживающего в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».
#903
Правильную игральную кость бросают дважды. Известно, что сумма выпавших очков больше 8. Найдите вероятность события "при втором броске выпало 4 очка".
#548
Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень дается не более двух выстрелов. Известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0,5. Найдите отношение вероятностей событий «стрелок поразить ровно пять мишеней» и «стрелок поразит ровно три мишени».
#935
Родительский комитет закупил 10 пазлов для подарков детям на окончание года, из них 2 с машинами и 8 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Андрюше достанется пазл с машиной.
#282
За круглый стол на 21 стул в случайном порядке рассаживаются 19 мальчиков и 2 девочки. Найдите вероятность того, что девочки не окажутся на соседних местах.
#714
В чемпионате мира по футболу участвуют 32 команды. С помощью жребия их делят на восемь групп по четыре команды в каждой. Группы называют латинскими буквами от А до Н. Какова вероятность того, что команда Франции окажется в одной из групп А, В, С или D?
#545
Агрофирма закупает куриные яйца в двух домашних хозяйствах. 35% яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 15% яиц высшей категории. Всего высшую категорию получают 30% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
#938
Телефон передает SMS-сообщение. В случае неудачи телефон делает следующую попытку. Вероятность того, что сообщение удастся передать без ошибок в каждой отдельной попытке, равна 0,2. Найдите вероятность того, что для передачи сообщения потребуется не больше двух попыток.
#923
Маша коллекционирует принцесс из Киндер-сюрпризов. Всего в коллекции 10 разных принцесс, и они равномерно распределены, то есть в каждом очередном Киндер-сюрпризе может с равными вероятностями оказаться любая из принцесс. У Маши уже есть шесть разных принцесс из коллекции. Какова вероятность того, что для получения следующей принцессы Маше придется купить еще 1 или 2 шоколадных яйца?
#925