-
Решения
-
Теория
-
Задачник
-
Идеи для учителя
- Заказать обучение
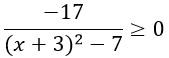
Преобразуем знаменатель и раскроем скобки по формуле сокращенного умножения "Квадрат суммы": (a + b)2 = a2 + 2ab + b2.
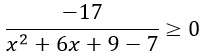
Приведем подобные слагаемые.
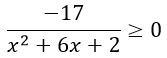
Поскольку неравенство квадратное, то нам необходимо разложить знаменатель на множители по формуле ax2 + bx + c = a(x - x1)(x - x2). Для этого решим квадратное уравнение:
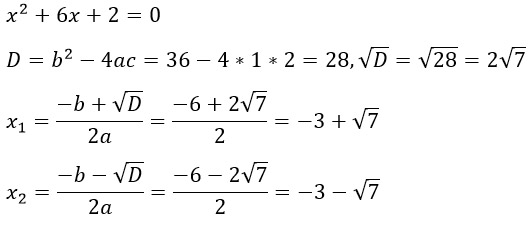
Неравенство примет вид, немного грустный)
Домножим обе его части на -1, чтобы избавится от минуса в числителе (Это делать не обязательно, кстати, но тогда дальнейшее решение будет слегка отличатся. На ответ это не влияет.). Не забываем, что при умножении/делении неравенства на отрицательное число, его знак меняется.
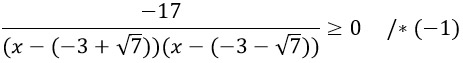
Преобразуем немного знаменатель...
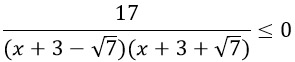
Метод интервалов! Отметим на числовой прямой точки, при которых знаменатель обращается в ноль. Они будут выколотые, т.к. знаменатель нулю равняться не может.
Из этих трех промежутков выбираем произвольные числа, подставляем в неравенство и определяем его знак. Получится вот такая штука:
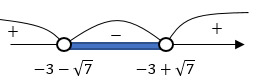
В нашем неравенстве стоит знак "меньше или равно", значит выбираем отрицательный промежуток.
![]()
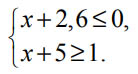


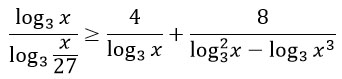
Укажите решение неравенства х2-36>0.
1) (-∞; +∞) 2) (-6; 6) 3) (-∞; -6)∪(6; +∞) 4) нет решений