Алгебра (7-11 класс)

Геометрия (7-11 класс)

Решите ой-ой-ой какое неравенство с логарифмами из книги Ященко, задание 15, ЕГЭ по математике.

Решение:

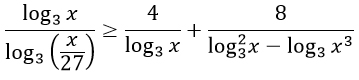
Преобразуем знаменатель первой дроби по свойству логарифмов: логарифм частного равен разности логарифмов.

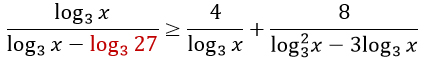
Сделаем замену.

Уравнение примет вид:

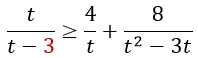
Приведем дроби к общему знаменателю t(t - 3) и перенесем всё в левую часть неравенства.

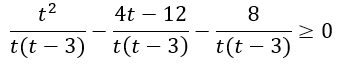
Объединим числители и приведем подобные слагаемые.

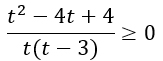
Разложим числитель дроби на множители по формуле сокращенного умножения "Квадрат разности" (также можно просто найти корни квадратного уравнения).

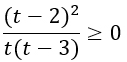
На числовой прямой отметим числа, при которых дробь в левой части неравенства обращается в ноль.

Точки 0 и 3 будут выколотыми, т.к. знаменатель не может быть равен 0.

Точка 2 будет закрашенная, т.к. неравенство нестрогое.

Определяем знаки промежутков.

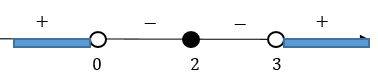
В неравенстве стоит знак "больше или равно", поэтому выбираем положительные промежутки и делаем обратную замену. Находим значения х, при которых неравенство будет верным.

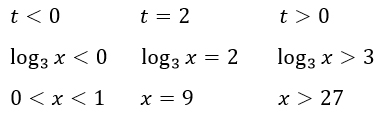
Ответ: (0; 1) U {9} U (27; +∞).

#дроби #неравенства #логарифмы #логарифмические неравенства

#710

ТОП 15 примеров из раздела "Неравенства и их системы"

Укажите решение системы неравенств х + 2,6 ≤ 0, x + 5 ≥ 1.

21.08.2019

39555

смотреть решение ...

#508

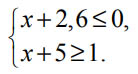
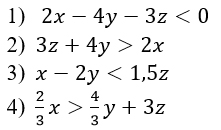
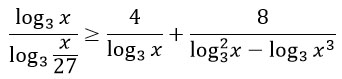
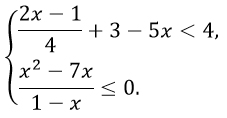
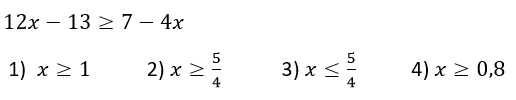
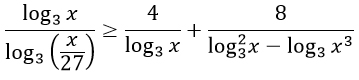
Укажите решение неравенства -2х+5<=-3x-3.

31.10.2019

30097

смотреть решение ...

#667

Решите неравенство -17/((х+3)^2-7)>=0.

30.04.2020

29380

смотреть решение ...

#772

Укажите неравенство, которое не имеет решений: 1) x^2+9x-79<0; 2) x^2+9x+79>0; 3) x^2+9x+79<0; 4) x^2+9x-79>0.

10.03.2020

25035

смотреть решение ...

#749

Какое из следующих неравенств не следует из неравенства 2x-4y<3z?

08.03.2019

11080

смотреть решение ...

#340

Решите неравенство (x^2-4x+3)/(x^4-x^6)≤0.

01.03.2019

9597

смотреть решение ...

#344

Решите неравенство (log по основанию 3 числа x)/(log по основанию 3 числа x/27) больше или равно (4/(log по основанию 3 числа x))+(8/log в квадрате по основанию 3 числа x - log по основанию 3 числа x в кубе).