Решите неравенство -13/(х^2+2x-8)<=0.

Решение:

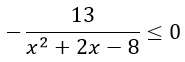
Обе части неравенства умножим на -1. При этом знак неравенства изменится на противоположный.

Разложим знаменатель на множители по формуле

ax² + bx + c = a(x - x₁)(x - x₂).

По теореме Виета выясняем, что корнями данного трехчлена будут числа -4 и 2, значит, неравенство можно перезаписать так:

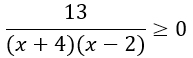
На числовой прямой отмечаем числа, при которых знаменатель обращается в 0 (точки будут выколотыми, т.к. знаменатель нулю равняться не может).

Определяем знаки промежутков (берем произвольное число из правого промежутка, например, 3, подставляем в неравенство и прикидываем знак результата. Он будет положительным - ставим плюс. Аналогично, с двумя другими промежутками).

В неравенстве стоит знаки "≥", значит, нас интересуют положительные промежутки.

Ответ: (-∞; -4) ∪ (2; +∞).

#дроби #неравенства

#705

ТОП 15 примеров из раздела "Неравенства и их системы"

Укажите решение системы неравенств х + 2,6 ≤ 0, x + 5 ≥ 1.

21.08.2019

41456

смотреть решение ...

#508

Решите неравенство -17/((х+3)^2-7)>=0.

30.04.2020

31993

смотреть решение ...

#772

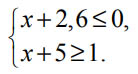
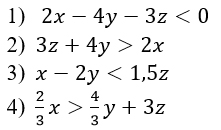
Укажите решение неравенства -2х+5<=-3x-3.

31.10.2019

30822

смотреть решение ...

#667

Укажите неравенство, которое не имеет решений: 1) x^2+9x-79<0; 2) x^2+9x+79>0; 3) x^2+9x+79<0; 4) x^2+9x-79>0.

10.03.2020

26654

смотреть решение ...

#749

Какое из следующих неравенств не следует из неравенства 2x-4y<3z?

08.03.2019

11470

смотреть решение ...

#340

Решите неравенство (x^2-4x+3)/(x^4-x^6)≤0.

01.03.2019

10212

смотреть решение ...

#344

Решите неравенство (log по основанию 3 числа x)/(log по основанию 3 числа x/27) больше или равно (4/(log по основанию 3 числа x))+(8/log в квадрате по основанию 3 числа x - log по основанию 3 числа x в кубе).