Векторы и операции над ними

Вектор – направленный отрезок.

 – противоположные ()

 – единичный вектор, длина равна 1. Единичный вектор, направление которого совпадает с направлением вектора a называется ортом.

Векторы  называются коллинеарными, если они лежат на прямой или параллельных прямых  Коллинеарные векторы могут быть направлены одинаково или противоположно.

Два вектора равны, если они коллинеарны, одинаково направлены и имеют одинаковые длины.

Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или 2 любые коллинеарны, то такие векторы компланарны.

Сумма.

Правило треугольника.

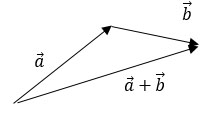
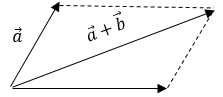
Правило параллелограмма.

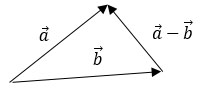
Разность.

Произведением  на скаляр  называется вектор   который имеет длину  коллинеарен  имеет направление вектора  если  и противоположное направление, если 

Свойства: 

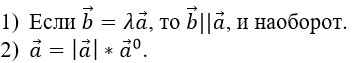
(каждый вектор равен произведению его модуля на орт)

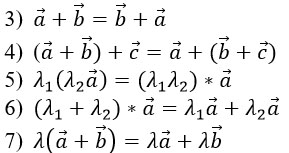
Проекцией вектора  на ось L  называется положительное число  если вектор  и L одинаково направлены и отрицательное число если и L противоположно направлены. Если A₁ и B₁ совпадают (т.е.  - нулевой), то проекция

Обозначение: 

Угол 0≤φ≤π – угол между вектором  и осью L.

Свойства проекций:

1) 

2) Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось.

3) При умножении вектора  на число λ его проекция на ось также умножается на это число.

Разложение вектора по ортам.

Пусть .

Обозначим проекции вектора  на оси:

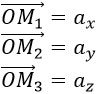
 - разложение вектора по ортам координатных осей.

Длина (модуль) вектора .

Сумма квадратов направляющих косинусов.

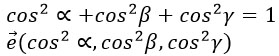
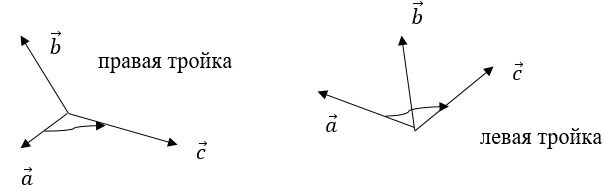
Действия над векторами, заданными проекциями.

 

Если кратчайший поворот от  идет против часовой стрелки, то тройка векторов правая, если по часовой – левая.

Векторным произведением  называется  который:

1) перпендикулярен вектору а и вектору b;

2) – угол между векторами а и b, т.е. имеет длину численно равную площадь параллелограмма, построенного на a и b как на сторонах;

3) векторы a, b и c образуют правую тройку.

Свойства:

Площади фигур через векторное произведение.

 

 

Смешанное (векторно-скалярное) произведение.

 построенного на этих векторах, взятому со знаком «+», если векторы образуют правую тройку, и со знаком «-», если левую.

Свойства:

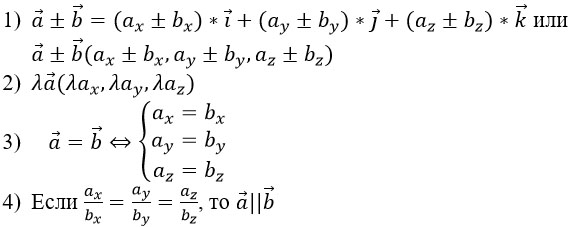
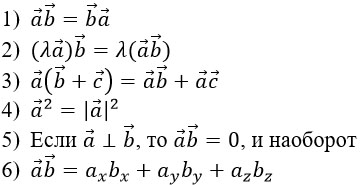
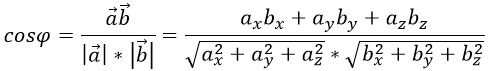
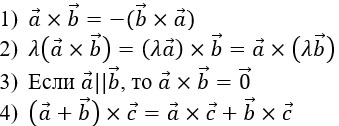
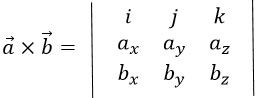
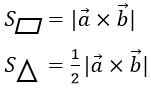
При подготовке к экзамену ориентируйтесь на лекции преподавателя.

Материал взят из книги Д.Письменного "Лекции по высшей математике". Опечатки маловероятны.

С уважением, Васильева Анна.