Докажите, что диагональ четырехугольника меньше его полупериметра.

Решение:

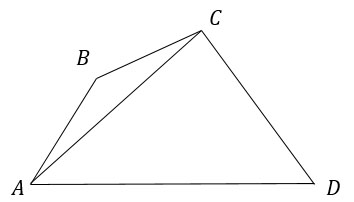
Дано:

ABCD - четырехугольник

АС - диагональ

Доказать: АС < p.

Доказательство:

Запишем формулу для нахождения полупериметра четырехугольника:

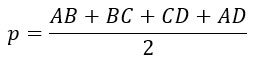
Неравенство треугольника гласит: длина любой стороны всегда меньше суммы двух других сторон.

В треугольнике АВС АС < АВ + ВС.

В треугольнике ACD АС < AD + CD.

Сложим эти два неравенства:

2АС < АВ + ВС + AD + CD.

Разделим обе части на 2 и получится, что

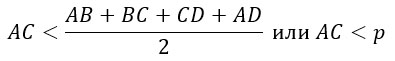
Что и требовалось доказать.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.

#четырехугольники

#266

ТОП 15 примеров из раздела "Многоугольники"

Известно, что около четырехугольника ABCD можно описать окружность и что продолжения сторон AD и ВС четырехугольника пересекаются в точке К. Докажите, что треугольники КАВ и KCD подобны.

12.10.2020

39886

смотреть решение ...

#842

В выпуклом четырехугольнике ABCD углы ABD и ACD равны. Докажите, что углы DAC и DBC также равны.

07.04.2021

24381

смотреть решение ...

#882

Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. Ответ дайте в квадратных сантиметрах.