Вычислите интеграл int((2x^5+6x^3+1)/(x^4+3x^2))dx.

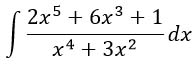
Под знаком интеграла находится неправильная дробь, т.к. в числителе старшая степень многочлена пятая, а в знаменателе - четвертая. Нам надо выделить целую часть. Сделать это можно разделив числитель на знаменатель или другим способом, который я тут применила: просто представила эту дробь в виде суммы двух других.

Для этого надо знаменатель разложить на простые множители и преобразовать числитель вот так:

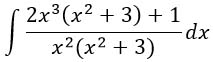
Видишь в числителе нарисовалась сумма? Еще со школы при сложении дробей с одинаковыми знаменателями мы складывали только числители. Нам надо сделать наоборот. Разбить сумму (результат сложения) на два слагаемых. Получаем, что интеграл суммы равен сумме интегралов:

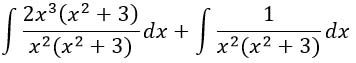
В первом интеграле дробь сокращается и числовой множитель 2 выносится за знак интеграла.  Во втором интеграле - правильная дробь.

__________________________

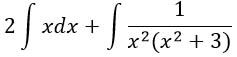
Сейчас пойдут отдельные вычисления.

Первый интеграл нас устраивает - он табличный. Работаем сейчас только со вторым. Воспользуемся методом неопределенных коэффициентов: разложим подынтегральную функцию в сумму элементарных дробей.

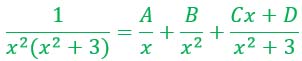
Приводим правую часть зеленого равенства к общему знаменателю.

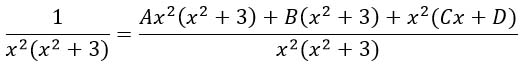
Т.к. знаменатели одинаковы, то обе части этого так называемого уравнения можно на него домножить и останутся только числители (поменяю левую и правую части местами для удобства):

Раскрываем скобки:

Разбираемся с числовыми коэффициентами. В левой части перед х⁴ стоит некоторое число А, а в правой части никаких иксов в четвертой степени не стоит. Но мы же можем изощрятся как угодно и подписать там x⁴, умноженный на ноль! Уравнение силу свою не утратит, а мы можем А сравнять с нулем.

Понижаем степень... Перед х³ стоит число С. По аналогии с предыдущими умозаключениями, оказывается, что С тоже равно 0.

Далее...Коэффициентов перед х² у нас несколько, все они положительны, значит записываем их все через "+". Их сумма также равна 0.

И, наконец, собираем в кучу свободные члены. В левой части - 3В, в правой части - 1. Приравниваем.

Получили систему уравнений:

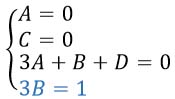
Решаем ее:

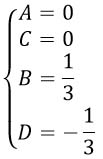
Подставляем найденные коэффициенты в зеленое равенство:

__________________________

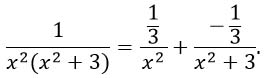
И теперь возвращаемся к решению нашего интеграла.

Разложенную функцию во втором интеграле запишем как сумму интегралов (я две дроби преобразовала чутка :) ):

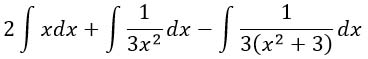
Из второго и третьего интеграла выносим вперед числовые коэффициенты, а сами подынтегральные выражения подводим к табличному виду:

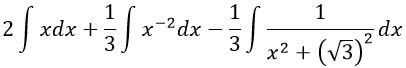
Используя таблицу интегралов получаем вот это чудо:

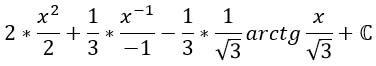
Преобразуем посимпатичнее и ответ готов!

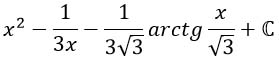
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.