Вычислите интеграл int(x*arctagx)dx.

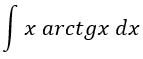
Воспользуемся методом замены переменной по формуле

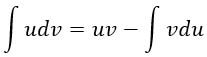
Пусть

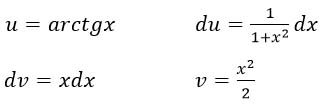
Тогда

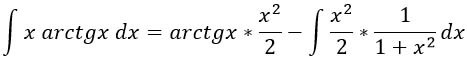
У произведения и интеграла вынесем ½. Получится вот такая симпотиШная запись:

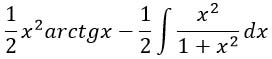
Далее работаем только с интегралом. Преобразуем числитель в подынтегральном выражении таким образом, чтобы в числителе оказалось то же самое выражение, что и в знаменателе.

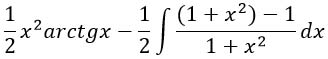
Разобьем дробь на разность единицы и получившейся после преобразований дроби.

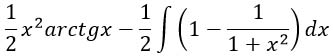
Интеграл разности равен разности интегралов. Не забудь оба интеграла умножить на -½.

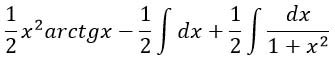
Вычисляем оба интеграла по таблице.

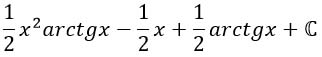
Преобразуем получившееся выражение.

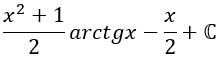
Все записи пиши через "=".

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.