Две касающиеся внешним образом в точке К окружности, радиусы которых равны 22 и 33, касаются сторон угла с вершиной А. Общая касательная к этим окружностям, проходящая через точку К, пересекает стороны угла в точках В и С. Найдите радиус окружности, описанной около треугольника АВС.

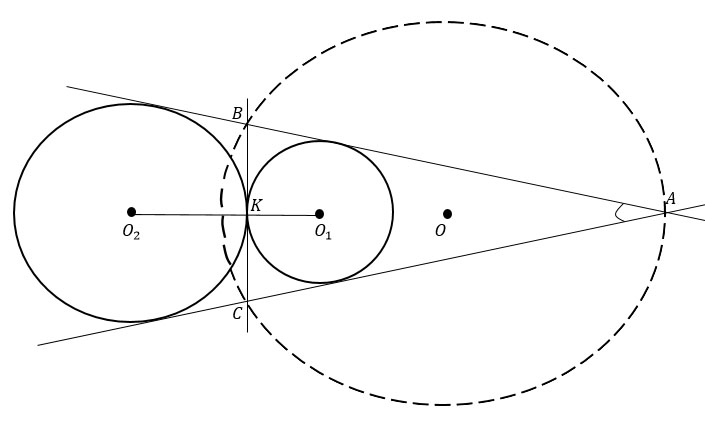
Дано:

окр. (О₁, О₁К)

окр. (О₂, О₂К)

окр. (О, АО)

О₁К = 22

О₂К = 33

∠А

АВ, АС, ВС - касательные, К ∈ ВС

Доказать: ΔАВС - равнобедренный

Найти: АО

Решение:

Проведем радиус малой окружности ЕО₁ ⊥ АВ и радиус средней окружности FО₂ ⊥ АВ (радиусы, проведенные в точки касания, перпендикулярны касательной).

Проведем О₁О₂ = О₁К + О₂К = ЕО₁ + FO₂ = 22 + 33 = 55 (все радиусы каждой окружности равны).

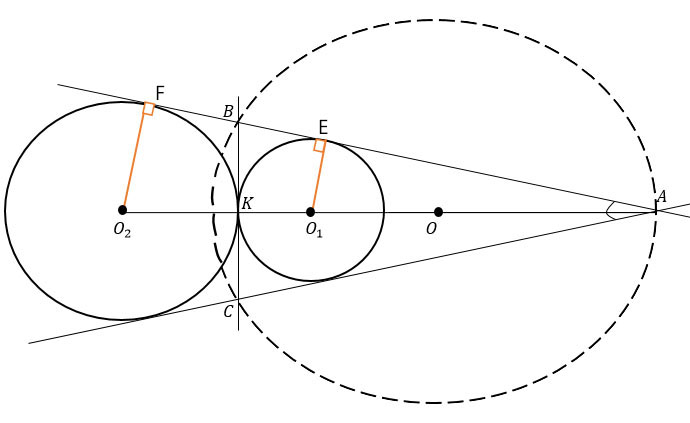
Рассмотрим ΔАЕО₁ и ΔАFО₂: ∠А - общий, ∠АЕО₁ = ∠АFО₂ = 90°, следовательно ΔАЕО₁ ∼ ΔАFО₂ по двум углам.

Если треугольники подобны, то стороны одного из них пропорциональны сходственным сторонам другого. Найдем АО₁:

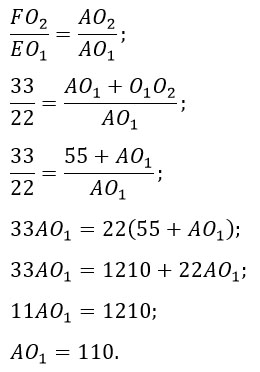
Найдем синус угла ЕАО₁. Он нам пригодится. Синус - это отношение противолежащего катета к гипотенузе, значит, из треугольника ЕАО₁

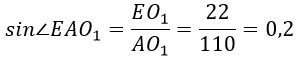
Найдем также длину отрезка АК:

АК ⊥ ВС, т.к. АК - продолжение радиусов О₁К и О₂К, а ВС - касательная, а мы знаем, что радиус, проведенный в точку касания, перпендикулярен касательной.

ВС - хорда большой окружности с центром О. АК делаит ВС пополам (т.к. радиус, перпендикулярный хорде, делит эту хорду пополам), т.е. ВК = КС.

Уберем с рисунка все лишнее, оставив треугольник АВС. Рассмотрим его.

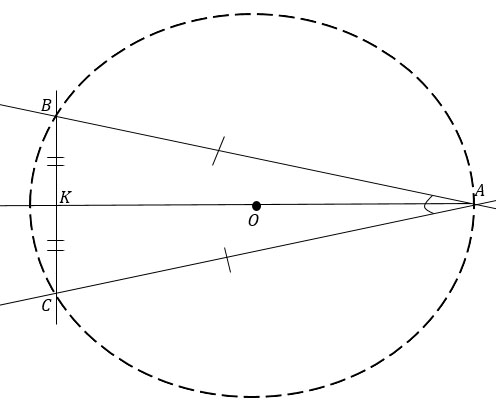
ΔАВС - равнобедренный, т.к. АК - медиана и высота.

Выпишу все, что мы знаем об этом треугольнике: АК = 132, sin∠BAO = 0,2.

АК также является биссектрисой, значит центр окружности О находится на ней, т.е. О ∈ АК.

ΔАВК - прямоугольный (АК ⊥ ВС), найдем АВ², используя теорему Пифагора.

АВ² = ВК² + АК²;

АВ² = (АВsin∠BAO)² + АК²; 

*если из равенства sin∠BAO = ВК/АВ выразить ВК, то получится АВsin∠BAO

АВ² = АВ²sin²∠BAO + АК²;

АВ² - АВ²sin²∠BAO = АК²;

АВ²(1 - sin²∠BAO) = АК²;

АВ²(1 - 0,2²) = 132²;

И оформим красивенько:

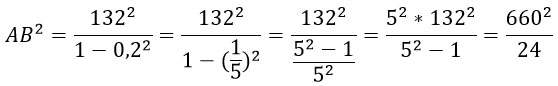
В треугольнике АВК проведем радиус ОВ и высоту ОН.

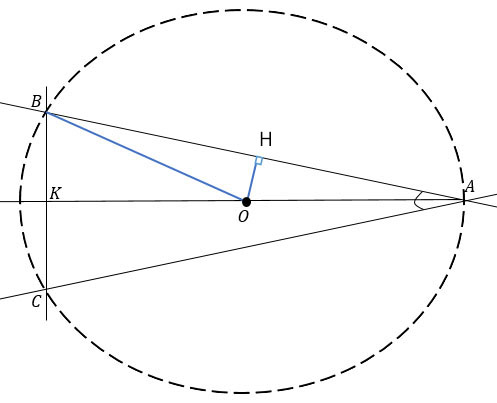
Рассмотрим треугольник АОВ: АО = ОВ - радиусы, значит ΔАОВ - равнобедренный. Тогда высота ОН будет являться еще и медианой, т.е. АН = НВ.

Из равенства sin∠ВАО = ОН/АО выразим ОН: ОН = 0,2 · АО.

Т.к. ΔАОН - прямоугольный, то по теореме Пифагора найдем АО:

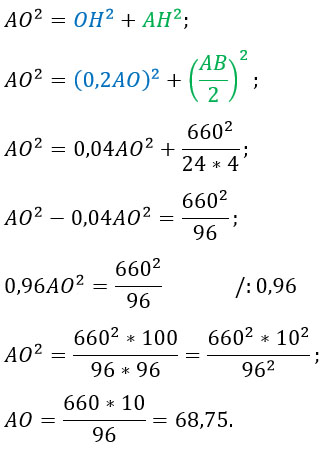
Ответ: 68,75.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.