Основание AC равнобедренного треугольника ABC равно 12. Окружность радиусом 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC . Найдите радиус окружности, вписанной в треугольник ABC.

Дано: 

ΔАВС - равнобедренный

АС = 12

окр. (О₁, О₁М)

окр. (О₂, О₂М)

О₂М = 8

М - точка касания

Найти: О₁М.

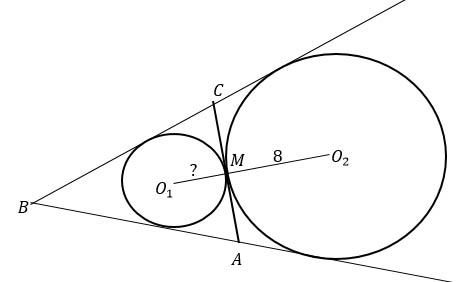
Решение:

Проведем радиусы О₁К и О₂Р в точки касания К и Р.

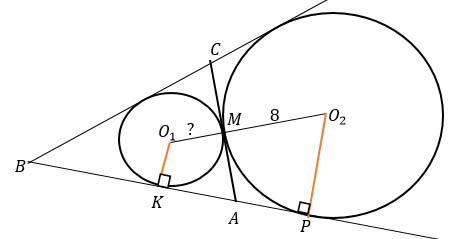
Сразу заметим, что радиусы, проведенные в точку касания, перпендикулярны касательной, и если две прямые перпендикулярны третьей, то они параллельны, т.е. О₁К || О₂Р. Следовательно, четырехугольник КО₁О₂Р - прямоугольная трапеция.

Проведем в трапеции высоту О₁Н.

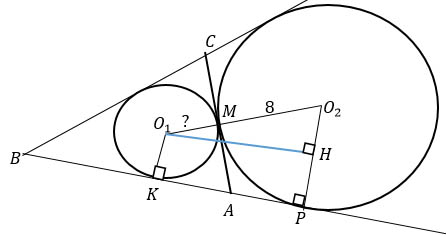
Получившийся треугольник О₁О₂Н  - прямоугольный.

Из условия задачи мы знаем, что М - середина АС, значит АМ = АС/2 = 12/2 = 6.

АК = АМ = АР = 6, т.к. отрезки касательных к окружности, проведенные из одной точки равны. Тогда КР = КА + АР = 6 + 6 = 12 = О₁Н (т.к. О₁КРН - прямоугольник).

Выразим катет О₂Н через О₁М: О₂Н = О₂Р - НР = О₂Р - О₁К = 8 - О₁М (О₁К = НР, т.к. О₁КРН - прямоугольник; О₁К = О₁М как радиусы одной и той же окружности).

Выразим гипотенузу через О₁М: О₁О₂ = О₁М + 8.

По теореме Пифагора

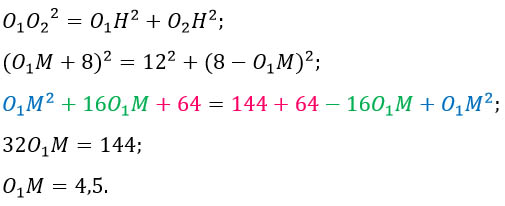
Ответ: 4,5.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.