В треугольнике АВС известны длины сторон АВ=40, АС=64, точка О - центр окружности, описанной около треугольника АВС. Прямая BD, перпендикулярная прямой АО, пересекает сторону АС в точке D. Найдите CD.

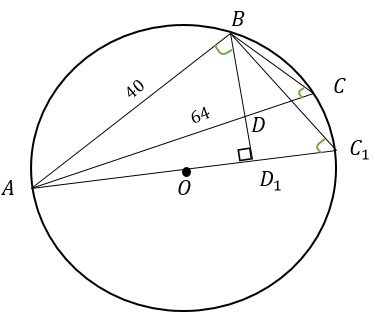
Дано:

ΔАВС

окр. (О; ОА) - описанная вокруг ΔАВС

BD⊥АО

BD∩AC=D (BD пересекает АС в точке D)

АВ=40, АС=64

Найти: СD.

Решение:

Прямая АО пересекает окружность в точках А и С₁. Т.к. АО - радиус, значит АС₁ - диаметр окружности.

Построим треугольник АВС_1.

∠АС₁В и ∠АСВ - вписанные и опираются на одну и ту же дугу АВ, значит ∠АС₁В=∠АСВ.

∠АВС₁ опирается на диаметр АС₁, значит ∠АВС₁=90º и ΔАВС₁ - прямоугольный.

В ΔАВС₁ высота BD₁, проведенная к гипотенузе АС₁, делит ΔАВС₁ на два ему подобных треугольника, т.е. ΔАВС₁ ∼ ΔАВD₁ ∼ ΔВD₁С₁. Из подобия следует, что ∠AC₁B=∠DBA=∠ACB.

Рассмотрим ΔABD и ΔACB: ∠ABD=∠ACB, ∠BAC - общий, значит ΔABD ∼ ΔACB по двум углам.

В подобных треугольниках стороны одного треугольника пропорциональны сходственным сторонам другого. Отсюда

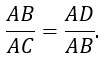
Подставляем известные величины в пропорцию и находим AD:

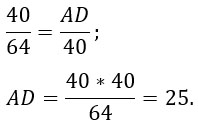
Теперь найдем CD.

CD=AC-AD=64-25=39.

Ответ: 39.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.