На стороне BC остроугольного треугольника ABC ( AB ≠ AC ) как на диаметре построена полуокружность, пе­ре­се­ка­ю­щая высоту AD в точке M, AD=90, MD=69, H — точка пересечения высот треугольника ABC. Найдите AH.

Для решения задачи достаточно провести 2 высоты: AD и BD₁. Они пересекутся в точке Н.

Продолжим высоту AD. Ее продолжение пересечет окружность в точке D₂.

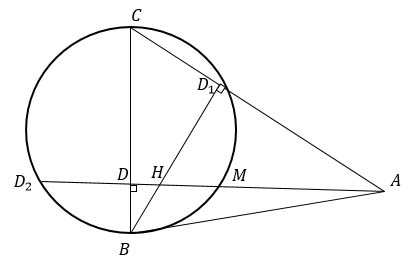
Т.к. ВС – диаметр и AD₂ ⊥ ВС, то DD₂ = МD = 69.

АС и АD₂ – секущие окружности. По теореме о секущих произведение одной из них на ее внешнюю часть равно произведению другой на ее внешнюю часть, т.е. AD₂ · AM = AC · AD₁.

Найдем AD₂ и AM:

AD₂ = AD + DD₂ = 90 + 69 = 159;

AM = AD₂ - MD - MD₂ = 159 - 69 - 69 = 21.

Значит, 159 · 21 = AC · AD₁ = 3339

ΔAD1H ∼ ΔADC по двум углам (∠А – общий, ∠AD₁H = ∠ADC = 90°). Из подобия треугольников следует, что

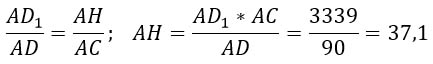
Ответ: 37,1.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.