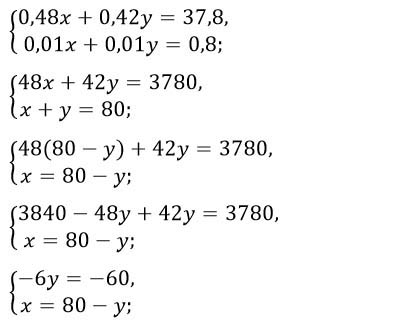Имеются два сосуда, содержащие 48 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 42% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько процентов кислоты содержится во втором растворе?
Решение:
В химических задачах, как правило, известны 2 показателя по каждому из растворов: процентное содержание кислоты и его масса. Эти данные мы будем записывать в прямоугольники, причем во всех прямоугольниках проценты будут сверху, а масса - снизу.
Т.к. растворы смешиваются, то прямоугольники будем рисовать через знаки "+", а тот, который получится в результате смешиваний - через "=". Это поможет нам легко составить уравнения.
Поехали!
Пусть х% - концентрация первого раствора, а у% - концентрация второго (указали это в первых двух прямоугольниках).
Т.к. эти растворы смешали, то масса получившегося 42%-ого раствора равна 48 + 42 = 90 кг (третий прямоугольник).
Теперь всё, что находится в прямоугольниках умножаем, не забыв проценты перевести в десятичные дроби, и составляем уравнение ("умножение дает нам возможность найти массу вещества в растворе", - говорит нам химия):

Во втором случае смешивают уже равные массы растворов. Давайте, для простоты вычислений, возьмем растворы по 1 кг. Заметьте, что концентрация этих двух растворов по-прежнему равна х% и у%. При их смешивании получаем 40%-ый раствор, массой 1 + 1 = 2 кг. Запишем эти данные в прямоугольники и аналогично, составляем второе уравнение.
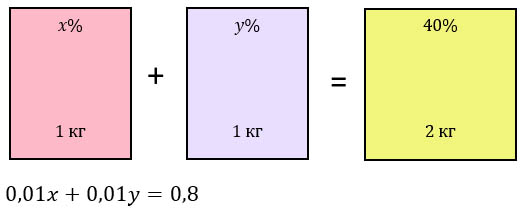
Решаем получившуюся систему уравнений:
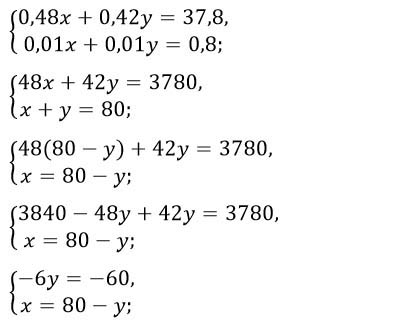
И в итоге получается, что y = 10% - концентрация второго раствора, х = 70% - концентрация первого.
Ответ: 10%.
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.
#534
ТОП 15 примеров из раздела "Текстовые задачи"
Смешав 45-процентный и 97-процентный растворы кислоты и добавив 10 кг чистой воды, получили 62-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 72-процентный раствор кислоты. Сколько килограммов 45-процентного раствора использовали для получения смеси?
#528
Первая труба пропускает на 5 литров воды в минуту меньше, чем вторая труба. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 200 литров она заполняет на 2 минуты дольше, чем вторая труба?
#731
Первая труба пропускает на 9 литров воды в минуту меньше, чем вторая труба. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 112 литров она заполняет на 4 минуты быстрее, чем первая труба?
#729
Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого автомобилиста на 17 км/ч, а вторую половину пути проехал со скоростью 102 км/ч, в результате чего прибвл в В одновременно в первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 65 км/ч.
#699
Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в город В на 10 часов раньше, чем велосипедист приехал в город А, а встретились они через 3 часа 45 минут после выезда. Сколько часов затратил на путь из города В в город А велосипедист?
#926
Семья состоит из мужа, жены и их дочери-студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 51%. Если бы стипендия дочери уменьшилась вдвое, общий доход семьи сократился бы на 3%. Сколько процентов от этого дохода составляет зарплата жены?
#920
Имеются два сосуда, содержащие 30 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 81% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 83% кислоты. Сколько килограммов кислоты содержится во втором растворе?
#498
Имеются два сосуда, содержащие 48 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 42% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько процентов кислоты содержится во втором растворе?
#534
Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 36 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 120 км, скорость первого велосипедиста равна 10 км/ч, скорость второго – 20 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
#724
Первую половину пути автомобиль проехал со скоростью 42 км/ч, а вторую – со скоростью 48 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
#490
Дорога между пунктами А и В состоит из подъема и спуска, а ее длина равна 22 км. Путь из А в В занял у туриста 8 часов, из которых 3 часов ушло на спуск. Найдите скорость туриста на спуске, если она больше скорости на подъеме на 2 км/ч. Ответ дайте в км/ч.
#893
Теплоход проходит по течению реки до пункта назначения 80 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 23 часа, а в пункт отправления теплоход возвращается через 35 часов после отплытия из него.
#730
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 42 килограммов изюма, если виноград содержит 82% воды, а изюм содержит 19% воды?
#921
Два велосипедиста одновременно отправились в 240-километровый пробег. Первый ехал со скоростью на 1 км/ч большей, чем скорость второго, и прибыл к финишу на 1 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.
#894
Моторная лодка прошла против течения реки 221 км и вернулась обратно в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.
#750