-
Решения
-
Теория
-
Задачник
-
Идеи для учителя
- Заказать обучение
Сейчас я покажу вам отличный и довольно-таки простой способ решения, казалось бы, таких страшных задач.
В них, как правило, известны 2 показателя по каждому из растворов: процентное содержание кислоты и его масса. Эти данные мы будем записывать в прямоугольники, причем во всех прямоугольниках проценты будут сверху, а масса - снизу.
Т.к. растворы смешиваются, то прямоугольники будем рисовать через знаки "+", а тот, который получится в результате смешиваний - через "=". Это поможет нам легко составить уравнения.
Поехали!
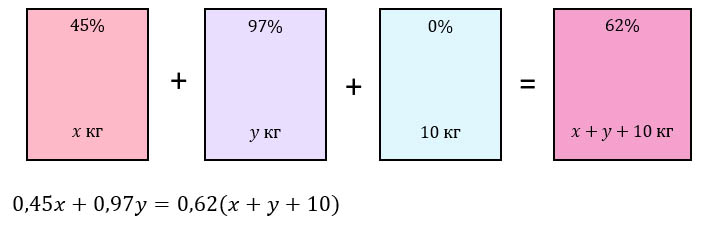
Пусть х - масса 45%-ого раствора, а у - масса 97%-ого раствора (указали это в первых двух прямоугольниках).
Процентное содержание кислоты в 10 кг воды - 0% (третий прямоугольник).
Т.к. 2 раствора и воду смешали, то масса получившегося 62%-ого раствора равна (х + у + 10) кг (четвертый прямоугольник).
Теперь всё, что находится в прямоугольниках умножаем, не забыв проценты перевести в десятичные дроби, и составляем уравнение ("умножение дает нам возможность найти массу вещества в растворе", - говорит школьный курс химии):
Теперь в первые 2 раствора вливают не воду, а 50%-ый раствор и на выходе получаем 72%-ый раствор массой (х + у + 10) кг. Меняем содержимое третьего и четвертого прямоугольников. Затем, точно так же, как и в первом случае, составляем уравнение.

Получили систему уравнений:
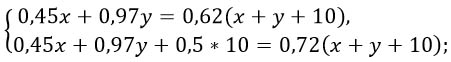
Для удобства умножим оба уравнения на 100. Это поможет нам избавится от десятичных дробей. Далее раскроем скобки и приведем подобные слагаемые:
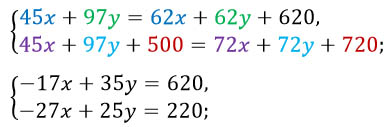
Выразим икс и подставим его во второе уравнение:
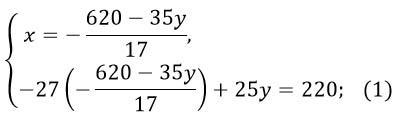
Чтобы не тащить за собой систему, решим второе уравнение отдельно и найдем игрек - массу второго раствора:
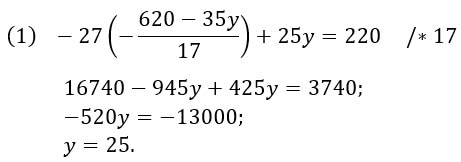
Осталось найти икс - массу первого раствора.
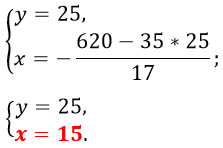
Ответ: 15 кг
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.