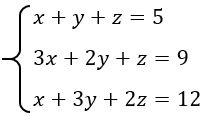Алгебра (7-11 класс)

Геометрия (7-11 класс)

Решить систему линейных уравнений с помощью обратной матрицы: x+y+z=5, 3x+2y+z=9, x+3y+2z=12.

Решение:

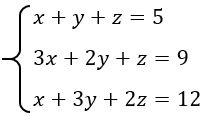
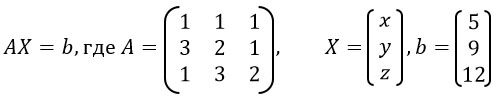
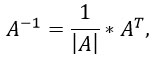
где |A| - определитель, А^Т - транспонированная матрица алгебраических дополнений соответствующих элементов матрицы А.

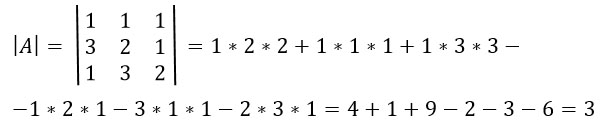
Находим матрицу М миноров:

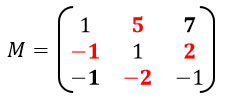
Меняем знаки у красных чисел и переставляем три пары чисел: 1 и -5, 2 и -2, -1 и 7 (тут мы знаки не меняли). Получаем транспонированную матрицу:

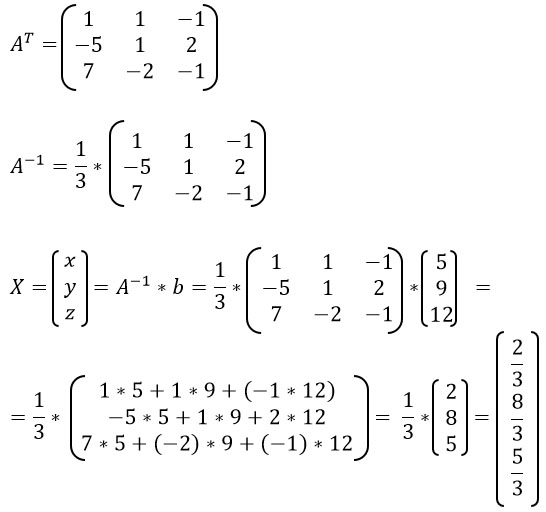
Ответ: 2/3, 8/3, 5/3.

Проверка:

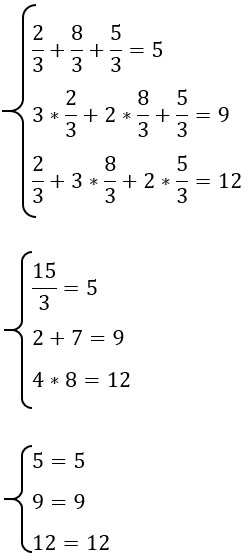
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.

#матрицы #системы уравнений

#177

ТОП 15 примеров из раздела "Системы линейных уравнений"

Решите систему линейных уравнений методом Крамера: 2x1-x2-x3=4, 3x1+4x2-2x3=11, 3x1-2x2+4x3=11.

18.02.2020

13715

смотреть решение ...

#748

Решите систему линейных уравнений методом Гаусса: 2x1-x2+3x3=-4, x1+3x2-x3=11, x1-2x2+2x3=-7.

08.10.2019

9016

смотреть решение ...

#616

Решите систему линейных уравнений методом Крамера: 3x1-2x2+4x3=21, 3x1+4x2-2x3=9, 2x1-x2-x3=10.

08.10.2019

7314

смотреть решение ...

#614

Решить систему линейных уравнений методом Крамера: x+y+z=5, 3x+2y+z=9, x+3y+2z=12.

18.06.2019

3685

смотреть решение ...

#178

Решить систему линейных уравнений методом Жордана-Гаусса: 2x1+x2+3x4=4, x1+x2+2x3+x4=3, x1+2x2+3x3-2x4=1, 4x1+3x2+6x3+2x4=8.

18.06.2019

3092

смотреть решение ...

#176

Решить систему линейных уравнений методом Жордана-Гаусса: 2x1+x2-x3=2, x1-2x2+5x3=3, x1+x2+3x3=-4, 2x1-3x2-6x3=19.

18.06.2019

2967

смотреть решение ...

#175

Решить систему линейных уравнений с помощью обратной матрицы: x+y+z=5, 3x+2y+z=9, x+3y+2z=12.

18.06.2019

2688

смотреть решение ...

#177

Алгебра (7-11 класс)

Геометрия (7-11 класс)

Решить систему линейных уравнений с помощью обратной матрицы: x+y+z=5, 3x+2y+z=9, x+3y+2z=12.

ТОП 15 примеров из раздела "Системы линейных уравнений"

Высшая математика