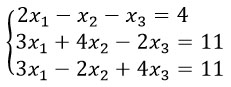Решите систему линейных уравнений методом Крамера: 2x1-x2-x3=4, 3x1+4x2-2x3=11, 3x1-2x2+4x3=11.

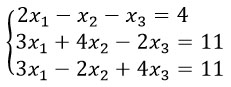
Решить эту систему методом Крамера сможет тот, кто знает как вычисляются определители матриц.

Напишу общую формулу для нахождения, чтобы в дальнейшем просто производить расчеты и не зацикливаться на расписывании того, что нужно умножать.

Итак, пусть дана матрица

Тогда ее определитель находится по формуле:

Переходим к нашей системе. Из коэффициентов, стоящих перед иксами, составим матрицу и найдем ее определитель.

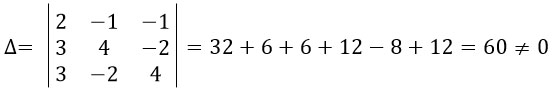
Определитель не равен 0, значит, методом Крамера пользоваться можно. 

Теперь, заменяя столбцы в исходной матрице на результаты уравнений (числа 4, 11 и 11), посчитаем определители по х₁, х₂ и х₃.

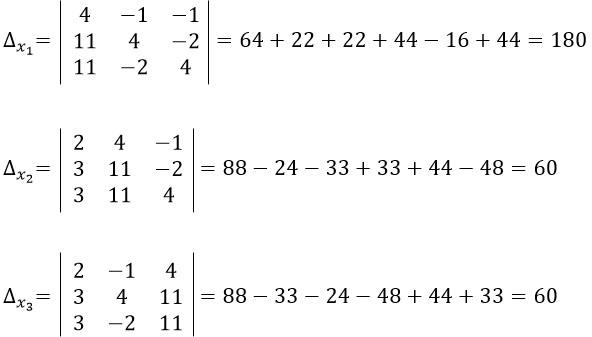
Последний этап - найдем корни уравнений.

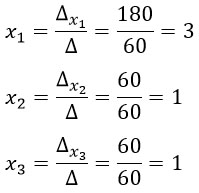
Обязательно следует сделать проверку, чтобы убедиться, что все сделано правильно.

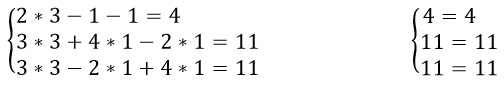
Ответ: 3, 1, 1.