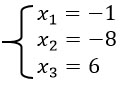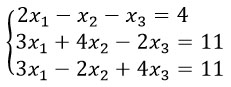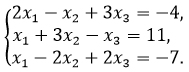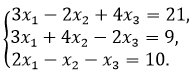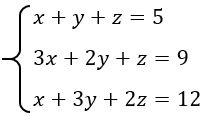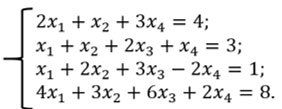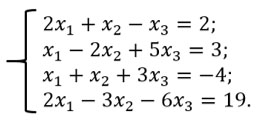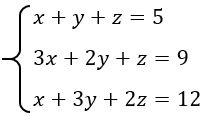Решить систему линейных уравнений методом Жордана-Гаусса: 2x1+x2+3x4=4, x1+x2+2x3+x4=3, x1+2x2+3x3-2x4=1, 4x1+3x2+6x3+2x4=8.

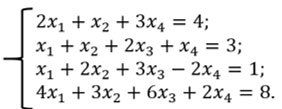
Составляем матрицу и с помощью элементарных преобразований приводим ее к виду

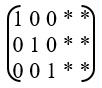
Обозначения: (1) – первая строка, (2) – вторая строка, (3) – третья строка, (4) – четвертая строка, 6(3) – третья строка, умноженная на 6. Запись всех матриц идет через «=».

Матрица будет выглядеть так:

Этап 1.

Из (4) вычитаем 2(1) или, по-другому, прибавляем -2(1).

Из (1) вычитаем (2). 

Из (3) вычитаем (2).

Получилась матрица:

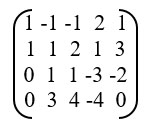
Этап 2.

К (1) прибавляем (3).

Из (2) вычитаем (1).

Из 3(3) вычитаем (4).

Получилась матрица:

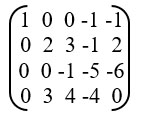
Этап 3.

(2) делим на 2.

Этап 4.

Из (4) вычитаем 3(2).

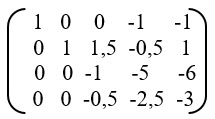
Этап 5.

Ко (2) прибавляем 3(4).

(4) умножаем на -1.

(3) умножаем на -1.

Этап 6.

Строки (3) и (4) пропорциональны. Вычеркиваем одну из них.

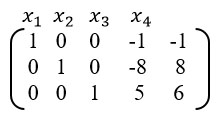
Этап 7.

Возвращаемся к системе уравнений:

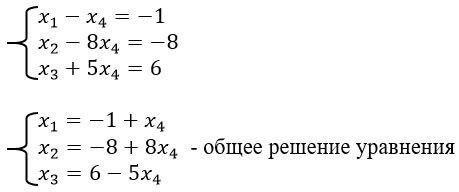
Частный случай. 

Если x₄=0 , то