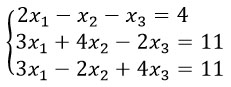Решите систему линейных уравнений методом Гаусса: 2x1-x2+3x3=-4, x1+3x2-x3=11, x1-2x2+2x3=-7.

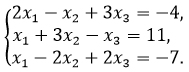
Составим расширенную матрицу:

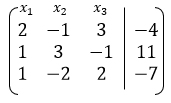
С помощью элементарных преобразований приведем ее к ступенчатому виду.

Обозначения: (1) – первая строка, (2) – вторая строка, (3) – третья строка, 2(3) – третья строка, умноженная на 2. Запись всех матриц идет через «=».

Этап 1.

Из (3) вычитаем (2)

Получилась матрица: 

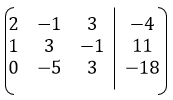
Этап 2.

Из 2(2) вычитаем (1).

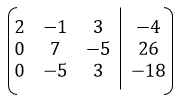
Этап 3.

(2) умножаем на 5.

(3) умножаем на 3. 

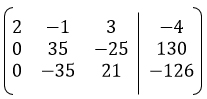
Этап 4.

К (3) прибавляем (2).

Затем (2) делим на 5. 

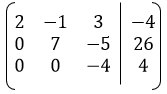
Этап 5.

(1) делим на 2.

(2) делим на 7.

(3) делим на -4. 

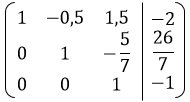
Этап 7.

Возвращаемся к системе уравнений.

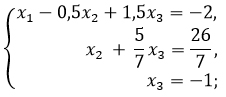
Решаем ее и находим корни уравнений.

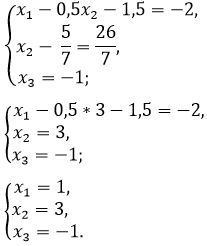
Проверка.

Подставляем найденный корни вместо иксов в исходную систему.

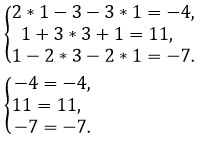
Ответ: 3; ±1.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.