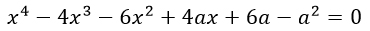Найдите все значения а, при каждом из которых уравнение x^4-4x^3-6x^2+4ax+6a-a^2=0 имеет не менее трех корней.

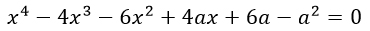
В этом задании левую часть уравнения необходимо разложить на множители так, чтобы в результате получилось уравнение вида a · b=0.

Для удобства я выделила разными цветами те одночлены, которые можно удачно сгруппировать.

Группируем :)

Первая скобка ни что иное, как формула сокращенного умножения «Разность квадратов». Разложим скобку на множители.

Выносим общий множитель (х² - а) за скобку.

Произведение равно 0 тогда, когда один из множителей равен 0, т.е.

Из уравнений выразим параметр а.

Графики этих двух уравнений представляют собой параболы. Их нам и надо построить.

Строим координатную плоскость с осями Ох и Оа.

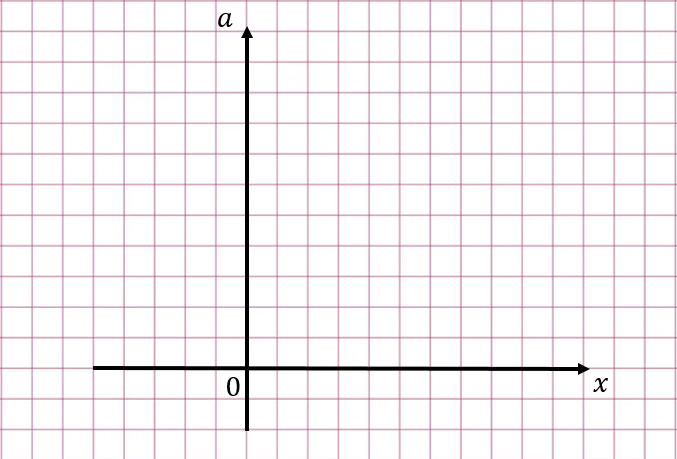
График уравнения а = х² имеет вершину в начале координат и ветви этой параболы направлены вверх.

Ветви графика второго уравнения а = -х² + 4х + 6 направлены вниз, а вершину надо найти.

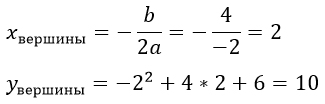
 Начертим оба графика.

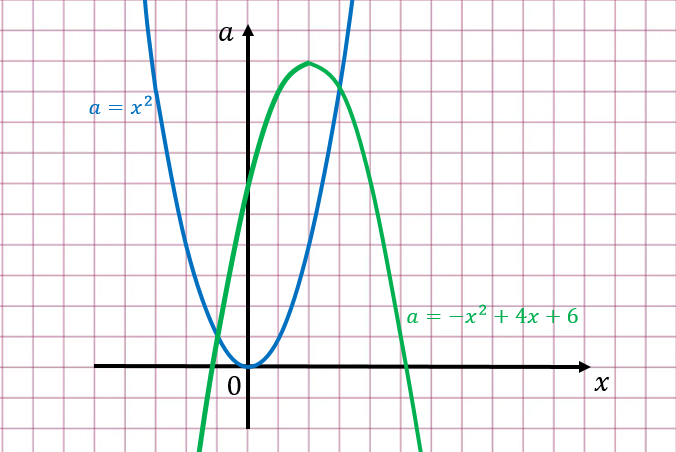
По графику хорошо видно, при каких значениях а уравнение имеет 3 и больше корней.

Ответ: 0≤а≤10.

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.