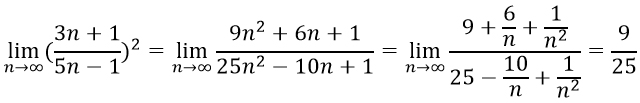Решить предел последовательности lim ((3n+1)/(5n-1))^2 при n, стремящемся к бесконечности.

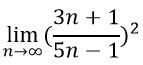
Возводим числитель и знаменатель дроби в квадрат по формуле квадрат/разность суммы: (a±b)²=a²±2ab+b².

Подставляя вместо n бесконечность видим, что получается какая-то ерунда, а именно, неопределенность вида ∞/∞. Чтобы от нее избавится нужно каждое слагаемое из числителя и знаменателя разделить на n в наибольшей степени.

В данном примере делим на n². Теперь, подставляя бесконечность вместо n, можно предположить, что дроби будут стремится к 0 (чем больше число в знаменателе, тем меньше дробь).