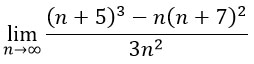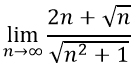-
Решения
-
Теория
-
Задачник
-
Идеи для учителя
- Заказать обучение
Подставляем вместо n бесконечность и получаем неопределенность вида ∞/∞. Чтобы от нее избавится надо числитель и знаменатель разделить на n в старшей степени.
Смотрим в числитель. Здесь старшая степень равна 1, т.к. корень из n можно заменить на n в степени ½, что меньше 1.
В знаменателе старшая степень будет такая же: отбросив единицу в подкоренном выражении у нас останется квадратный корень из n², а он равен n.
Деление на n в числителе не составляет труда, а вот со знаменателем надо не ошибиться. Т.к. знаменатель содержит корень, мы не можем взять и разделить все содержимое в корне на n. Надо n сначала внести под знак корня, другими словами возвести n в квадрат, а потом уже делить. В записи решения это отражено. А дальше - дело техники.
Получившиеся после деления дроби стремятся к 0 потому, что знаменатель бесконечно увеличивается. Остаются только числа 2 в числителе и 1 в знаменателе, которые нужно поделить.
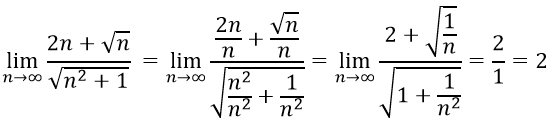
Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.